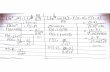
transformasi-laplace

TRANSFORMASI LAPLACE

VIII. 1.DEFINISI

Misalkan f ( t ) terdefinisi untuk semua t≥0 , maka transformasi Laplace dari f ( t )

dirumuskan :

L{f ( t )}=

F (s )=∫0

∞

e−st f ( t )dt(8.1)

Fungsi F (s )disebut transformasi Laplace dari fungsif ( t )dan dilambangkan L{f ( t )} dan

inversnya dilambangkan dengan L-1{F (s )}=f ( t ).Catatan : fungsi asli dalam kawasan waktu ditulis dengan huruf kecil sedangkan hasil

transformasinya ditulis dengan huruf kapital. Contoh Y ( s ) adalah transformasi Laplace

dari y ( t ) .

Contoh : f ( t )=1untuk t≥0 . Hitung F (s ) !Jawab :

F (s )=∫0

∞

e−st f ( t )dt

F (s )=∫0

∞

e−st . 1.dt

F (s )=[−1s

e−st ]0

∞

=1s

, dengan s>0

Latihan : hitung transformasi Laplace dar fungsi : y ( t )=eat untuk t≥0 .

VIII. 2.LINIERITAS TRANSFORMASI LAPLACE

Terdapat fungsi f ( t )dan g( t ) maka transformasi Laplace dari a . f (t )+b .g( t ) adalah

a . F( s )+b .G(s )

a . f (t )+b .g( t )↔a .F (s )+b .G(s ) (8.2)

Contoh : hitung Transformasi Laplace dari f ( t )=cosh at= eat+e−at

2 .

Jawab :

misalkan f ( t )=cosh at=eat+e−at

2=1

2{x ( t )+ y ( t )}=1

2x ( t )+1

2y ( t )

sehinggax ( t )=eat dan y ( t )=e−at

X ( s )=∫0

∞

e− ste at dt=∫0

∞

e−( s−a )t dt=[−1s−a

e−( s−a )t ]0

∞

=1s−a

untuk s>a>0

dengan cara yang sama diperoleh :

Y ( s )=1s+a

untuk s>0 , a>0

sehingga

F (s )=12X (s )+1

2Y ( s )=1

21s−a

+12

1s+a

=ss2−a2

Latihan :

Tentukan transformasi laplace dari fungsi berikut :

a. f ( t )=3 t+4

b. f ( t )=2cosωt

VIII. 3.TRANSFORMASI LAPLACE BEBERAPA FUNGSI DASAR

Tabel 8.1 Transformasi Laplace sinyal dasar

f ( t ) F (s )1 1

st 1

s2

t2 2!

s3

tn(n=1,2,3 , .. ) n !

sn+1

eat 1s−a

cosωt s

s2+ω2

sinωt ω

s2+ω2

cosh at s

s2−a2

sinhat a

s2−a2

Latihan : Hitung f ( t ) dari fungsi F (s ) beikut :

a.F (s )= 5

s+3

b.F (s )= 1

s4

c.F (s )= 2

s2+16

d.F (s )= s+1

s2+1

e.F (s )= s−4

s2−4

VIII. 4.TRANSFORMASI LAPLACE DARI TURUNAN

Jika f ( t ) kontinu untuk t≥0 dan f ' ( t )adalah turunan dari f ( t ) maka transformasi

Laplace dari f ' ( t ) adalah

L{f ' ( t )}=sF (s )−f (0) (8.3)

Contoh :

v ( t )=sinωt ,t≥0

i(0 )=1

Gambar 8.1

v ( t )=Lδi ( t )δ ( t )

+Ri( t )

Transformasi Laplace dari dua ruas persamaan di atas :

L{v ( t )}= L {Lδi ( t )δ ( t )

+Ri ( t )}= L.L {

δi( t )δ( t ) }+ R. L{i( t )}

ω

s2+ω2 = L {s.I(s) - i(0)} + R.I(s)

ω

s2+ω2 = L.s.I(s) – L.i(0) + R.I(s)

ω

s2+ω2 = {L.s + R }.I(s) – L.1.

{L.s + R }.I(s) =

ω

s2+ω2 + L

I (s )=

ω

s2+ω2+L

Ls+R

Secara umum :

Jika f ( t )dan turunannya merupakan fungsi kontinu untuk t≥0 , maka :

L{f(n)( t )}=snF( s )−sn−1 f (0)−sn−2 f ' (0 )−. ..−f (n−1)(0) (8.4)

VIII. 5.TRANSFORMASI LAPLACE DARI INTEGRAL

Jika f ( t ) kontinu maka :

L{∫0

t

f (τ )δτ}=

F ( s )s

, s>0(8.5)

Contoh :

Gambar 8.2

v ( t )=sinωt ,t≥0

Persamaan tegangan pada rangkaian tersebut adalah :

v ( t )=vC ( t )+vR( t )

v ( t )=1C∫ i( t )δt+R .i( t )

Transformasi Laplace dari persamaan di atas :

L{sinωt }=

1C L{∫ i( t )δt }+R.L{i(t)}

ωs2+ω2

=1CI ( s )s

+R . I (s )

ωs2+ω2

=(1Cs +R) . I (s )

sehingga diperoleh :

I (s )=

ω

s2+ω2

(1Cs +R)=ωcs

( s2+ω2)(1+RCs)

VIII. 6.SIFAT PERGESERAN FREKUENSI

Jika transformasi Laplace dari f ( t ) adalah F (s )dan jika g( t )=eat f ( t ) maka

transformasi Laplace dari g( t ) dirumuskan :

G( s )=F (s−a ) (8.6)

dengan syarat s>a

Contoh :

f ( t )=1 , untuk t≥0

maka F( s )=1s

g( t )=e5 t f ( t )=e5 t

maka G(s )=F ( s−5)=1s−5

dengan s>5

VIII. 7.SIFAT PERGESERAN WAKTU

Jika transformasi Laplace dari f ( t ) adalah F (s )dan jika g( t )=f ( t−a ) maka

transformasi Laplace dari g( t ) dirumuskan :

G( s )=e−asF ( s ) (8.7)

Contoh :

Gambar 8.3.

vC( t )=0 , untuk t<1 . Tentukan i( t )!Jawab :

v ( t )=vC ( t )+vR( t )

v ( t )=1C∫ i( t )δt+Ri( t )

V ( s )=I (s )Cs

+RI (s )

Dari gambar 8.3 diperoleh v ( t )=1 , untuk 1≤t≤2atau v ( t )=u( t−1)−u( t−2) sehingga

diperoleh V ( s )= e−s

s− e−2 s

s

Diperoleh :

e−s

s−e−2 s

s=I (s )(1Cs +R)

I (s )=

e−s

s−e−2 s

s

(1Cs +R)=e−s−e−2 s

s (Cs1+RCs )=e−s−e−2 s (1R

1RC

+s )sehingga diperoleh :

i( t )=1Re−

(t−1)RC u ( t−1 )−1

Re−

(t−2)RC u ( t−2)

Gambar 8.4

VIII. 8.TRANSFORMASI LAPLACE PADA FUNGSI PERIODIS

Gambar 8.5

Misalkan f ( t ) sinyal periodis dengan periode T>0sedemikian sehingga f ( t+T )=f ( t )

maka :

F (s )=∫0

T

e−st f ( t )δt

1−e−sT

(8.8)

Contoh :

Sinyal f ( t )={sin t ,0≤t≤π

0 , π≤t≤2 π periodis dengan periode 2.

a) Gambarkan sinyal f ( t )!

b) Tentukan transformasi Laplace dari f ( t )!Jawab :

a)

gambar 8.6

b) Transformasi Laplace dari f ( t )dihitung sebagai berikut :

F (s )=∫0

T

e−st f ( t )δt

1−e−sT

F (s )=∫0

π

e−st sin tδt

1−e−sT

F (s )=[e−st (−s sin t−cos t )s2+1 ]

0

π

1−e−s 2 π

F (s )=1

1−e−s 2 π (1+e−πs

s2+1 )=1

(1−e−sπ )( s2+1)

VIII. 9. INVERS TRANSFORMASI LAPLACE

Diberikan sebuah sinyal x ( t ) dengan hasil transformasi Laplacenya X ( s ), maka x ( t )

dapat dihitung dari X ( s ) dengan invers transformasi Laplace X ( s ). Invers transformasi

Laplace dihitung sebagai berikut :

x ( t )= 12πj

∫c− j∞

c+ j∞

X ( s )estds(8.9)

Integral pada persamaan 8.9 dihitung sepanjang kurva s=c+ jω pada bidang

kompleks dari c− j∞ sampai c+ j∞dengan c adalah sembarang bilangan riil yang

mana kurva s=c+ jω terletak pada daerah konvergensi (ROC).

Pada dasarnya terlalu sulit menghitung invers transformasi Laplace dengan persamaan

8.9, sehingga digunakan cara lain dengan menggunakan pecahan parsial dan tabel

transformasi Laplace sinyal dasar.

VIII. 10. INITIAL VALUE PROBLEM

Contoh : Tentukan f ( t )jika diketahui persamaan diferensial sebagai berikut :

f ''+4 f '+3 f=0f (0)=3f ' (0 )=1

Jawab :

L{f ''+4 f '+3 f }=L{0}

L{f '' }= s2F−sf (0 )−f ' (0 )=s2F−3 s−1

L{f ' }= sF−f (0)=sF−3

Sehingga diperoleh persamaan :

s2F−3 s−1+4 ( sF−3 )+3 F=0(s2+4 s+3 )F=3 s+1+12

F=3 s+13

s2+4 s+3=

3 s+13( s+3 )(s+1)

Dengan pecahan parsial :

F=As+3

+Bs+1

As+3

+Bs+1

=A ( s+1 )+B( s+3 )( s+3 )(s+1)

=( A+B) s+(A+3B )(s+3 )(s+1)

sehingga diperoleh persamaan :( A+B) s+(A+3B )=3 s+13A+B=3 .. . .. ..( pers. 1)A+3B=13 .. .. . .(pers .2 )(pers .1 )−(pers .2 ) diperoleh : -2B=-10B=5A=-2

Y=-2s+3

+5s+1

sehingga diperoleh :y ( t )=-2e-3t+5e-t

VIII. 11. APLIKASI PADA RANGKAIAN LISTRIK

Gambar 8.7 Rangkaian RLC sederhana

Rangkaian listrik sederhana seperti gambar 8.7 terdiri atas elemen rangkaian yang

terhubung seri dengan saklar K. Elemen tersebut adalah :

Sumber tegangan E (volt)

Resistor R (ohm)

Induktor L (henry)

Kapasitor C (farad)

Ketika saklar K ditutup, maka muatan Q (coulomb) akan mengalir ke kapasitor.

Kecepatan aliran muatan tersebut :

δqδt

=i( t )(8.10)

disebut sebagai arus (dengan satuan ampere).

Masalah terpenting adalah menentukan muatan pada kapasitor dan arus sebagai fungsi

waktu. Untuk itu didefinisikan tegangan drop pada elemen rangkaian sebagai berikut :

vR( t )=i( t )R=Rδq ( t )δt

vL( t )=Lδi( t )δt

=Lδ2 i( t )δt2

vC( t )=q ( t )C

= 1C∫ i( t )δt

(8.11)

(8.12)

(8.13)

Kemudian digunakan hokum kirchoff untuk mendapatkan persamaan diferensial.

Untuk rangkaian gambar 8.7 diperoleh :

vS ( t )=vC ( t )+vR( t )+vL( t )

vS ( t )=q ( t )C

+Rδq ( t )δt

+Lδ2q ( t )δt2

atau

vS( t )=1C∫ i( t )δt+Ri( t )+L

δi( t )δt

Contoh :

Gambar 8.8

Sebuah induktor 2 henry dan kapasitor 0,02 farad dihubungkan seri dengan resistor 16

ohm dan sumber tegangan E volts. Pada t = 0, muatan kapsitor dan arus pada

rangkaian adalah nol. Tentukan muatan dan arus untuk t > 0, jika :

a. E = 300 volts

b. E = 100 sin 3t volts

Jawab :

Misalkan q(t) dan i(t) adalah muatan dan arus sesaat. Dengan hukum kirchoff

diperoleh :

e ( t )=vC (t )+vR( t )+vL (t )

e ( t )=q ( t )C

+Rδq( t )δt

+Lδ2q( t )δt2

Dengan kondisi awal q(0) = 0, i(0 )=0=q '(0 )

a. Jika E = 300 volts

300=q ( t )0,02

+16δq( t )δt

+2δ2q (t )δt2

Dengan transformasi Laplace diperoleh :

300s

=Q0,02

+16 (sQ−q( 0))+2 (s2Q−sq(0 )−q ' (0 ))

300s

=50Q+16 sQ+2 s2Q

300s

=2(25+8 s+s2 )Q

Q=150s (25+8 s+s2 )

150

s(25+8 s+s2 )=As

+Bs+C(25+8 s+s2 )

A=150

(25+8 s+s2)|s=0=

15025

=6

Untuk s=1diperoleh

15034

=6+B+C34

⇔−54=B+C .. .. . .( pers .1 )

Untuk s=2diperoleh

15090

=3+ 2B+C45

⇔−60=2 B+C .. .. .. ( pers .2 )

(pers. 1) – (pers. 2) diperoleh : 6=−B⇔B=−6 sehingga diperoleh C=−48

sehingga :

Q=6s−6 s+48

(25+8 s+s2 )=6s

−6( s+4 )+24

( s+4 )2+9=6s

−6( s+4 )( s+4 )2+9

−24( s+4 )2+9

sehingga : q ( t )=6−6e−4 t cos3 t−8e−4 t sin 3 t

i( t )=δq( t )δt

=24e−4 t cos3 t+18e−4 t sin 3 t+32e−4 t sin 3 t−24 e−4t cos3 t=50e−4 t sin 3 t

b. Silahkan dicoba

Latihan :

1. Sebuah resistor R ohm dan kapasitor C farad dihubungkan seri dengan sumber

tegangan E volts. Saat t = 0, muatan kapasitor juga nol. Tentukan muatan dan arus

untuk t > 0, jika :

a. E = E0

b. E = E0e-at, a>0

Gambar 8.9

2. Perhatikan gambar berikut :

Gambar 8.10

E = 500 sin 10t volts

R1 = R2 =10 ohm

L = 1 Henry

C = 0,01 farad

Jika muatan kapasitor dan arus i1 dan i2 bernilai nol saat t = 0, tentukan muatan

kapasitor saat t > 0.

LATIHAN 5

Sebuah sistem mempunyai impuls respon h( t )=3(u( t )−u ( t−2)) .

a. Tentukan transformasi laplace dari h( t ) !

b. Tentukan keluaran sistem y ( t ) jika diberi masukan sinyal x ( t )=10δ ( t ).

c. Tentukan keluaran sistem y ( t ) jika diberi masukan sinyal x ( t )=10u( t )

d. Tentukan keluaran sistem y ( t ) jika diberi masukan sinyal x ( t )=10sin 50 t