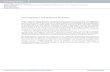
Ideal Gases 1L =1 dm 3 = 0.001 m 3 1L=1000 cm 3 , cc, mL 1m 3 =1000 dm 3 =10 6 cm 3 RT V P nRT PV 1 Chapter 16: The Properties of Gases

Statistical Thermodynamics Chapter 16
Oct 20, 2015
Equations of state
Welcome message from author
This document is posted to help you gain knowledge. Please leave a comment to let me know what you think about it! Share it to your friends and learn new things together.
Transcript

Ideal Gases
1L =1 dm3= 0.001 m3
1L=1000 cm3, cc, mL 1m3 =1000 dm3 =106 cm3
RTVPnRTPV
1
Chapter 16: The Properties of Gases

Gas Constant
2

Real Gases versus Ideal Gases
3
300 K
CH4

Van der Waals, Redlich-Kwong, Peng-Robinson
4

5

6

Van der Waals, Redlich-Kwong, Peng-Robinson
vdw ??
ethane at 400 K
ethane at 305.33 K
7

Experimental P-V isotherms of CO2
8

Cubic Equations of State describe both liquid and gaseous region
9

Critical values of Pc , Vc , and Tc for vwd EOS
Critical values of Pc , Vc , and Tc for R-K EOS
10
27
8 27
3 2 bRaT
baPbV ccc

The value of is constant !!
11

The constant values of EOS can be obtained from Pc and Tc
12

Law of Corresponding States (LOCS)
13

Based on LOCS, all gases have the same functional
14

Virial Equation of State
15

Experimental Determination of B2V
B2V and Temperature
16

Relationships between virial coefficients and intermolecular interactions
r
Lennard-Jones Potential
17

18

Divide both sides by
B2V and LOCS
19
xr/TkT B VH /*

@ T* | 3.2 , B2v (T*) =0
B*2V vs T* and Boyle Temperature
20

The second virial coefficient indicates the first deviation from ideal gas
21

Three contributions to attractive force
22

Hard-Sphere Potential
23

Square-Well Potential
24

Relationship between B2V and a, b coefficients in vdw EOS
25

Relationship between B2V and a, b coefficients in vdw EOS
drreNdrrNTB 2rTkc
A2
A6
B ]1[2 )1(2- )(
0v2
6
³³f
��� V
V
SS 1 / 66 ¢¢rTkc B
36
2
3 2
VS cNa A
32 3
ANb SV
26
"��� 2!xxe2
x 1
Related Documents