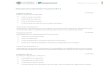
Marcelo De Jesús Delgado Del Carpio CUI: 20140525 Ingeniería Electrónica Cálculo en varias variables EXAMEN “D”: Capítulo 6, Sección 2 (Página 570) Ejercicio 11: Calcule la integral doble de la función f ( x,y) dada sobre el rectángulo Q. f ( x,y ) =x 2 ye xy ,Q=[ 0,1 ]∗[ 0,1] Solución: ∫ 0 1 ∫ 0 1 x 2 ye xy dydx ∫ 0 1 x 2 . [ ∫ 0 1 ye xy dy ] dx Integrando por partes: ∫ ye xy dy u=ydv=e xy dy du= dyv= 1 x .e xy ¿ > ∫ ye xy dy=¿ y x .e xy − 1 x . ∫ e xy dy ¿ ¿ y x .e xy − 1 x 2 .e xy + C ¿ e xy . ( y x − 1 x 2 ) +C Volviendo a la integral: ∫ 0 1 x 2 . [ e xy . ( y x − 1 x 2 ) ] 0 1 dx

Welcome message from author
This document is posted to help you gain knowledge. Please leave a comment to let me know what you think about it! Share it to your friends and learn new things together.
Transcript

Marcelo De Jesús Delgado Del Carpio CUI: 20140525 Ingeniería ElectrónicaCálculo en varias variables
EXAMEN “D”:
Capítulo 6, Sección 2 (Página 570)
Ejercicio 11:
Calcule la integral doble de la función f (x , y ) dada sobre el rectángulo Q.
f ( x , y )=x2 y exy ,Q=[ 0,1 ]∗[0,1]
Solución:
∫0
1
∫0
1
x2 ye xydydx
∫0
1
x2 .[∫01
ye xydy ]dxIntegrando por partes:
∫ y exy dy
u= y dv=exy dy
du=dy v=1x. exy
¿>∫ y exy dy=¿ yx. e
xy
−1x.∫e xydy ¿
¿ yx. exy
− 1x2 . e
xy+C
¿exy .( yx− 1x2 )+C
Volviendo a la integral:
∫0
1
x2 .[exy .( yx− 1x2 )]0
1
dx
∫0
1
x2 .[ex .( 1x− 1x2 )+ 1
x2 ]dx∫0
1
(x . ex−ex+1 )dx
[ex ( x−1 )−ex+x ]01

Marcelo De Jesús Delgado Del Carpio CUI: 20140525 Ingeniería ElectrónicaCálculo en varias variables
3−e∴
Capítulo 6, Sección 6 (Página 632)
Ejercicio 12:
Calcular la integral triple indicada.
∭Ω
(x e y+ ye z )dxdydz
Donde Ω es la región limitada por los planos x=0 , y=0 , z=0 , y=1−x , z=1
Solución:
1. Graficamos la región Ω:
2. Integramos sobre la región Ω:
∫0
1
∫0
1− x
∫0
1
(xe y+ y ez )dzdydx
∫0
1
∫0
1− x
[zx e y+ y ez ]01dydx
∫0
1
∫0
1− x
(xe y+ ye− y )dydx

Marcelo De Jesús Delgado Del Carpio CUI: 20140525 Ingeniería ElectrónicaCálculo en varias variables
∫0
1
[ xe y+ y2
2(e−1 )]
0
1−x
dx
∫0
1
[ xe y+ y2
2(e−1 )]
0
1−x
dx
∫0
1
(x e1− x+(1−x)2
2(e−1 )−x)dx
[e1− x (−1−x )−(1−x )3
6(e−1 )− x
2
2 ]0
1
76. e−8
3∴
Capítulo 6, Sección 7 (Página 645)
Ejercicio 16:
Calcule la integral triple indicada.
∭Ω
(x2+ y2 )dxdydz
Donde la región es:Ω=( x , y , z )∨x2+ y2≤1, x≥0 , y ≥0 ,−1≤ z≤1
Solución:
1. Graficamos la región Ω:
2. Llevamos a coordenadas cilíndricas:x=r cosθy=rsin θz=z
y
x
z

Marcelo De Jesús Delgado Del Carpio CUI: 20140525 Ingeniería ElectrónicaCálculo en varias variables
J=r(Jacobiano)3. Según la región:
0≤ r≤1
0≤θ≤ π2
−1≤z ≤14. Reemplazando y multiplicando por el jacobiano:
∫−1
1
∫0
1
∫0
π2
r3dθdrdz
∫−1
1
∫0
1
r3 [θ ]0π2 drdz
π2∫−1
1
∫0
1
r3drdz
π8∫−1
1
[r4 ]01dz= π
8 ∫−1
1
dz=π8
[z ]−11
= π4
∴
Related Documents