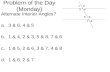
Problem of the Day Let f be a differentiable function such that f(3) = 2 and f '(3) = 5. If the tangent line to the graph of f at x = 3 is used to find an approximation to a zero of f, that approximation is A) 0.4 B) 0.5 C) 2.6 D) 3.4 E) 5.5

Problem of the Day
Jan 12, 2016
Problem of the Day. Let f be a differentiable function such that f(3) = 2 and f '(3) = 5. If the tangent line to the graph of f at x = 3 is used to find an approximation to a zero of f , that approximation is. A) 0.4 B) 0.5 C) 2.6 D) 3.4 E) 5.5. Problem of the Day. - PowerPoint PPT Presentation
Welcome message from author
This document is posted to help you gain knowledge. Please leave a comment to let me know what you think about it! Share it to your friends and learn new things together.
Transcript

Problem of the DayLet f be a differentiable function such that f(3) = 2 and f '(3) = 5. If the tangent line to the graph of f at x = 3 is used to find an approximation to a zero of f, that approximation is
A) 0.4B) 0.5C) 2.6D) 3.4E) 5.5

Problem of the DayLet f be a differentiable function such that f(3) = 2 and f '(3) = 5. If the tangent line to the graph of f at x = 3 is used to find an approximation to a zero of f, that approximation is
A) 0.4B) 0.5C) 2.6D) 3.4E) 5.5
Point (3, 2)Slope = 5Tangent y - 2 = 5(x - 3)Thus y = 5x - 13To find zero 0 = 5x - 13 x = 2.6

If h(x) = f(x)g(x) what is the derivative?

If h(x) = f(x)g(x) what is the derivative?
f(x + Δx)g(x + Δx) - f(x)g(x)Δx
add a well chosen zero
f(x+Δx)g(x+Δx) + f(x+Δx)g(x) - f(x+Δx)g(x) - f(x)g(x)Δx
lim Δx 0

If h(x) = f(x)g(x) what is the derivative?
f(x + Δx)g(x + Δx) - f(x)g(x)Δx
add a well chosen zero
f(x+Δx)g(x+Δx) - f(x+Δx)g(x) + f(x+Δx)g(x) - f(x)g(x) Δx
f(x+Δx)(g(x+Δx) - g(x)) + g(x)(f(x+Δx) - f(x)) Δx
lim Δx 0
lim Δx 0

If h(x) = f(x)g(x) what is the derivative?
f(x + Δx)g(x + Δx) - f(x)g(x)Δx
add a well chosen zero
f(x+Δx)g(x+Δx) - f(x+Δx)g(x) + f(x+Δx)g(x) - f(x)g(x) Δx
f(x+Δx)(g(x+Δx) - g(x)) + g(x)(f(x+Δx) - f(x)) Δx
lim Δx 0
lim Δx 0
f(x+Δx)(g(x+Δx) - g(x)) Δx
lim Δx 0
+ g(x)(f(x+Δx) - f(x))Δx
lim Δx 0

If h(x) = f(x)g(x) what is the derivative?
f(x+Δx) (g(x+Δx) - g(x)) Δx
lim Δx 0
+ g(x) (f(x+Δx) - f(x))Δx
lim Δx 0
Evaluate limits
f(x) g'(x) + g(x) f '(x)

If h(x) = f(x)g(x) what is the derivative?
f(x) g'(x) + g(x) f '(x)
1st times derivative of second + 2nd times derivative of
1st
Product Rule
(Rule extends to cover more than 2 factors)if j(x) = f(x)g(x)h(x) then
j'(x) = f '(x)g(x)h(x) + f(x)g'(x)h(x) + f(x)g(x)h'(x)

Find the derivative of y = 2xcos x - 2sin x

Find the derivative of y = 2xcos x - 2sin x
y' = 2x(-sinx) + cos x(2) - 2cos x
y' = -2xsin x

Quotient Rule(Proof is in textbook)
if h(x) = f(x) g(x)
then h'(x) = g(x)f '(x) - f(x)g'(x) (g(x))2

Quotient Rule(Proof is in textbook)
if h(x) = f(x) g(x)
HiLo
then h'(x) = g(x)f '(x) - f(x)g'(x) (g(x))2
Lo d Hi - Hi d Lo Lo Lo

Quotient Rule
Find the derivative of 7x2 - 4 3x4 - 2x

Quotient Rule
Find the derivative of 7x2 - 4 3x4 - 2x
(3x4 - 2x)(14x) - (7x2 - 4)(12x3 - 2)
(3x4 - 2x)2

Find the derivative of x2 + 3x 6
Find the derivative of 9 5x2
Find the derivative of -3(3x - 2x2) 7x

Caution! Not every quotient needs the quotient rule.
Find the derivative of x2 + 3x 6
y = 1 (x2 + 3x) 6
y' = 1 (2x + 3) 6

Find the derivative of 9 5x2
y = 9 x-2
5
y' = 9 (-2x-3) 5
y' = -18 5x3

Find the derivative of -3(3x - 2x2) 7x
y = -3(3 - 2x) 7
y' = -3(-2) 7
y' = -6 7

Trig Derivativesd tan x = sec2x dx
d sec x = secx tanx dx
d csc x = - cscx cotx dx
d cot x = - csc2x dx

Find the derivative of y = x2csc x

Find the derivative of y = x2csc x
y' = x2(-cscx cotx) + 2x(csc x) = (x cscx)(-x cotx + 2)
How do you know when you have finished?
Combine like terms and remove negative exponents.
Related Documents