NLopt Tutorial - AbInitio

NLopt

Download

Release notes

FAQ

NLopt manual

Introduction

Installation

Tutorial

Reference

Algorithms

License and Copyright

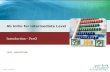
Feasible region for a simple example optimization problem with twononlinear (cubic) constraints.

NLopt Tutorial

From AbInitio

In this tutorial, we illustrate the usage of NLopt in various languages via one ortwo trivial examples.

Contents

1 Example nonlinearly constrained problem2 Example in C/C++

2.1 Number of evaluations2.2 Switching to a derivative-free algorithm

3 Example in C++4 Example in Matlab or GNU Octave

4.1 Matlab verbose output5 Example in Python

5.1 Important: Modifying grad in-place6 Example in GNU Guile (Scheme)7 Example in Fortran

Example nonlinearly constrained problem

As a first example, we'll look at thefollowing simple nonlinearly constrainedminimization problem:

subject to ,

, and

for parameters a1=2, b1=0, a2=-1, b2=1.

The feasible region defined by theseconstraints is plotted at right: x2 is

constrained to lie above the maximum of twocubics, and the optimum point is located atthe intersection (1/3, 8/27) where theobjective function takes on the value

.

(This problem is especially trivial, because

by formulating it in terms of the cube root of x2 you can turn it into a linear-programming problem, but we won't do

that here.)

In principle, we don't need the bound constraint x2≥0, since the nonlinear constraints already imply a positive-x2

feasible region. However, NLopt doesn't guarantee that, on the way to finding the optimum, it won't violate thenonlinear constraints at some intermediate steps, while it does guarantee that all intermediate steps will satisfy thebound constraints. So, we will explicitly impose x2≥0 in order to ensure that the √x2 in our objective is real.

Note: The objective function here is not differentiable at x2=0. This doesn't cause problems in the examples below,

but may cause problems with some other algorithms if they try to evaluate the gradient at x2=0 (e.g. I've seen it cause

AUGLAG with a gradient-based solver to fail). To prevent this, you might want to use a small nonzero lower bound

instead, e.g. x2≥10−6.

Example in C/C++

To implement the above example in C or C++, we would first do:

# i n c l u d e < m a t h . h >

# i n c l u d e < n l o p t . h >

to include the NLopt header file as well as the standard math header file (needed for things like the s q r t functionand the H U G E _ V A L constant), then we would define our objective function as:

d o u b l e m y f u n c ( u n s i g n e d n , c o n s t d o u b l e * x , d o u b l e * g r a d , v o i d * m y _ f u n c _ d a t a )

{

i f ( g r a d ) {

g r a d [ 0 ] = 0 . 0 ;

g r a d [ 1 ] = 0 . 5 / s q r t ( x [ 1 ] ) ;

}

r e t u r n s q r t ( x [ 1 ] ) ;

}

There are several things to notice here. First, since this is C, our indices are zero-based, so we have x [ 0 ] and x [ 1 ]instead of x1 and x2. The return value of our function is the objective . Also, if the parameter g r a d is not

N U L L , then we set g r a d [ 0 ] and g r a d [ 1 ] to the partial derivatives of our objective with respect to x [ 0 ] andx [ 1 ] . The gradient is only needed for gradient-based algorithms; if you use a derivative-free optimization algorithm,g r a d will always be N U L L and you need never compute any derivatives. Finally, we have an extra parameterm y _ f u n c _ d a t a that can be used to pass additional data to m y f u n c , but no additional data is needed here so thatparameter is unused.

For the constraints, on the other hand, we will have additional data. Each constraint is parameterized by two numbersa and b, so we will declare a data structure to hold this information:

t y p e d e f s t r u c t {

d o u b l e a , b ;

} m y _ c o n s t r a i n t _ d a t a ;

Then, we implement our constraint function as follows. (You always create a single constraint function, even if youhave several very different constraints—your constraint function can do different things depending on what is passedas the v o i d * d a t a parameter.)

d o u b l e m y c o n s t r a i n t ( u n s i g n e d n , c o n s t d o u b l e * x , d o u b l e * g r a d , v o i d * d a t a )

{

m y _ c o n s t r a i n t _ d a t a * d = ( m y _ c o n s t r a i n t _ d a t a * ) d a t a ;

d o u b l e a = d - > a , b = d - > b ;

i f ( g r a d ) {

g r a d [ 0 ] = 3 * a * ( a * x [ 0 ] + b ) * ( a * x [ 0 ] + b ) ;

g r a d [ 1 ] = - 1 . 0 ;

}

r e t u r n ( ( a * x [ 0 ] + b ) * ( a * x [ 0 ] + b ) * ( a * x [ 0 ] + b ) - x [ 1 ] ) ;

}

The form of the constraint function is the same as that of the objective function. Here, the d a t a parameter willactually be a pointer to m y _ c o n s t r a i n t _ d a t a (because this is the type that we will pass ton l o p t _ m i n i m i z e _ c o n s t r a i n e d below), so we use a typecast to get the constraint data. NLopt always

expects constraints to be of the form m y c o n s t r a i n t ([) ≤ 0, so we implement the constraint x2 ≥ (a x1 + b)3 as

the function (a x1 + b)3 − x2. Again, we only compute the gradient if g r a d is non-N U L L , which will never occur if

we use a derivative-free optimization algorithm.

Now, to specify this optimization problem, we create an "object" of type n l o p t _ o p t (an opaque pointer type) andset its various parameters:

d o u b l e l b [ 2 ] = { - H U G E _ V A L , 0 } ; / * l o w e r b o u n d s * /

n l o p t _ o p t o p t ;

o p t = n l o p t _ c r e a t e ( N L O P T _ L D _ M M A , 2 ) ; / * a l g o r i t h m a n d d i m e n s i o n a l i t y * /

n l o p t _ s e t _ l o w e r _ b o u n d s ( o p t , l b ) ;

n l o p t _ s e t _ m i n _ o b j e c t i v e ( o p t , m y f u n c , N U L L ) ;

Note that we do not need to set an upper bound (n l o p t _ s e t _ u p p e r _ b o u n d s ), since we are happy with thedefault upper bounds (+∞). To add the two inequality constraints, we do:

m y _ c o n s t r a i n t _ d a t a d a t a [ 2 ] = { { 2 , 0 } , { - 1 , 1 } } ;

n l o p t _ a d d _ i n e q u a l i t y _ c o n s t r a i n t ( o p t , m y c o n s t r a i n t , & d a t a [ 0 ] , 1 e - 8 ) ;

n l o p t _ a d d _ i n e q u a l i t y _ c o n s t r a i n t ( o p t , m y c o n s t r a i n t , & d a t a [ 1 ] , 1 e - 8 ) ;

Here, the 1 e - 8 is an optional tolerance for the constraint: for purposes of convergence testing, a point will be

considered feasible if the constraint is violated (is positive) by that tolerance (10−8). A nonzero tolerance is a goodidea for many algorithms lest tiny errors prevent convergence. Speaking of convergence tests, we should also set oneor more stopping criteria, e.g. a relative tolerance on the optimization parameters [:

n l o p t _ s e t _ x t o l _ r e l ( o p t , 1 e - 4 ) ;

There are many more possible parameters that you can set to control the optimization, which are described in detail bythe reference manual, but these are enough for our example here (any unspecified parameters are set to innocuousdefaults). At this point, we can call nlopt_optimize to actually perform the optimization, starting with some initial guess:

d o u b l e x [ 2 ] = { 1 . 2 3 4 , 5 . 6 7 8 } ; / * s o m e i n i t i a l g u e s s * /

d o u b l e m i n f ; / * t h e m i n i m u m o b j e c t i v e v a l u e , u p o n r e t u r n * /

i f ( n l o p t _ o p t i m i z e ( o p t , x , & m i n f ) < 0 ) {

p r i n t f ( " n l o p t f a i l e d ! \ n " ) ;

}

e l s e {

p r i n t f ( " f o u n d m i n i m u m a t f ( % g , % g ) = % 0 . 1 0 g \ n " , x [ 0 ] , x [ 1 ] , m i n f ) ;

}

n l o p t _ o p t i m i z e will return a negative result code on failure, but this usually only happens if you pass invalidparameters, it runs out of memory, or something like that. (Actually, most of the other NLopt functions also return anerror code that you can check if you are paranoid.) (However, if it returns the failure codeN L O P T _ R O U N D O F F _ L I M I T E D , indicating a breakdown due to roundoff errors, the minimum found may still beuseful and you may want to still use it.) Otherwise, we print out the minimum function value and the correspondingparameters x.

Finally, we should call nlopt_destroy to dispose of the n l o p t _ o p t object when we are done with it:

n l o p t _ d e s t r o y ( o p t ) ;

Assuming we save this in a file tutorial.c, we would compile and link (on Unix) with:

c c t u t o r i a l . c - o t u t o r i a l - l n l o p t - l m

The result of running the program should then be something like:

f o u n d m i n i m u m a t f ( 0 . 3 3 3 3 3 4 , 0 . 2 9 6 2 9 6 ) = 0 . 5 4 4 3 3 0 8 4 7

That is, it found the correct parameters to about 5 significant digits and the correct minimum function value to about 6significant digits. (This is better than we specified; this often occurs because the local optimization routines usually tryto be conservative in estimating the error.)

Number of evaluations

Let's modify our program to print out the number of function evaluations that were required to obtain this result. First,we'll change our objective function to:

i n t c o u n t = 0 ;

d o u b l e m y f u n c ( i n t n , c o n s t d o u b l e * x , d o u b l e * g r a d , v o i d * m y _ f u n c _ d a t a )

{

+ + c o u n t ;

i f ( g r a d ) {

g r a d [ 0 ] = 0 . 0 ;

g r a d [ 1 ] = 0 . 5 / s q r t ( x [ 1 ] ) ;

}

r e t u r n s q r t ( x [ 1 ] ) ;

}

using a global variable c o u n t that is incremented for each function evaluation. (We could also pass a pointer to acounter variable as m y _ f u n c _ d a t a , if we wanted to avoid global variables.) Then, adding a p r i n t f :

p r i n t f ( " f o u n d m i n i m u m a f t e r % d e v a l u a t i o n s \ n " , c o u n t ) ;

we obtain:

f o u n d m i n i m u m a f t e r 1 1 e v a l u a t i o n s

f o u n d m i n i m u m a t f ( 0 . 3 3 3 3 3 4 , 0 . 2 9 6 2 9 6 ) = 0 . 5 4 4 3 3 0 8 4 7

For such a simple problem, a gradient-based local optimization algorithm like MMA can converge very quickly!

Switching to a derivative-free algorithm

We can also try a derivative-free algorithm. Looking at the NLopt Algorithms list, another algorithm in NLopt thathandles nonlinear constraints is COBYLA, which is derivative-free. To use it, we just change N L O P T _ L D _ M M A("LD" means local optimization, derivative/gradient-based) into N L O P T _ L N _ C O B Y L A ("LN" means local optimization,no derivatives), and obtain:

f o u n d m i n i m u m a f t e r 3 1 e v a l u a t i o n s

f o u n d m i n i m u m a t f ( 0 . 3 3 3 3 2 9 , 0 . 2 9 6 2 ) = 0 . 5 4 4 2 4 2 3 0 1

In such a low-dimensional problem, derivative-free algorithms usually work quite well—in this case, it only triples thenumber of function evaluations. However, the comparison is not perfect because, for the same relative x tolerance of

10−4, COBYLA is a bit less conservative and only finds the solution to 3 significant digits.

To do a fairer comparison of the two algorithms, we could set the x tolerance to zero and ask how many functionevaluations each one requires to get the correct answer to three decimal places. We can specify this by using thes t o p v a l termination criterion, which allows us to halt the process as soon as a feasible point attains an objective

function value less than s t o p v a l . In this case, we would set s t o p v a l to , replacing

n l o p t _ s e t _ x t o l _ r e l with the statement:

n l o p t _ s e t _ s t o p v a l ( o p t , s q r t ( 8 . / 2 7 . ) + 1 e - 3 ) ;

corresponding to the last line of arguments to n l o p t _ m i n i m i z e _ c o n s t r a i n e d being s q r t ( 8 . / 2 7 . ) + 1 e -3 , 0 . 0 , 0 . 0 , 0 . 0 , N U L L , 0 , 0 . 0 . If we do this, we find that COBYLA requires 25 evaluations whileMMA requires 10.

The advantage of gradient-based algorithms over derivative-free algorithms typically grows for higher-dimensionalproblems. On the other hand, derivative-free algorithms are much easier to use because you don't need to worry abouthow to compute the gradient (which might be tricky if the function is very complicated).

Example in C++

Although it is perfectly possible to use the C interface from C++, many C++ programmers will find it more natural touse real C++ objects instead of opaque n l o p t _ o p t pointers, s t d : : v e c t o r < d o u b l e > instead of arrays, andexceptions instead of error codes. NLopt provides a C++ header file n l o p t . h p p that you can use for this purpose,which simply wraps a C++ object interface around the C interface above.

# i n c l u d e < n l o p t . h p p >

The equivalent of the above example would then be:

n l o p t : : o p t o p t ( n l o p t : : L D _ M M A , 2 ) ;

s t d : : v e c t o r < d o u b l e > l b ( 2 ) ;

l b [ 0 ] = - H U G E _ V A L ; l b [ 1 ] = 0 ;

o p t . s e t _ l o w e r _ b o u n d s ( l b ) ;

o p t . s e t _ m i n _ o b j e c t i v e ( m y f u n c , N U L L ) ;

m y _ c o n s t r a i n t _ d a t a d a t a [ 2 ] = { { 2 , 0 } , { - 1 , 1 } } ;

o p t . a d d _ i n e q u a l i t y _ c o n s t r a i n t ( m y c o n s t r a i n t , & d a t a [ 0 ] , 1 e - 8 ) ;

o p t . a d d _ i n e q u a l i t y _ c o n s t r a i n t ( m y c o n s t r a i n t , & d a t a [ 1 ] , 1 e - 8 ) ;

o p t . s e t _ x t o l _ r e l ( 1 e - 4 ) ;

s t d : : v e c t o r < d o u b l e > x ( 2 ) ;

x [ 0 ] = 1 . 2 3 4 ; x [ 1 ] = 5 . 6 7 8 ;

d o u b l e m i n f ;

n l o p t : : r e s u l t r e s u l t = o p t . o p t i m i z e ( x , m i n f ) ;

There is no need to deallocate the o p t object; its destructor will do that for you once it goes out of scope. Also, thereis no longer any need to check for error codes; the NLopt C++ functions will throw exceptions if there is an error,which you can c a t c h normally.

Here, we are using the same objective and constraint functions as in C, taking d o u b l e * array arguments.Alternatively, you can define objective and constraint functions to take s t d : : v e c t o r < d o u b l e > arguments if youprefer. (Using s t d : : v e c t o r < d o u b l e > in the objective/constraint imposes a slight overhead because NLopt mustcopy the d o u b l e * data to a s t d : : v e c t o r < d o u b l e > , but this overhead is unlikely to be significant in most realapplications.) That is, you would do:

d o u b l e m y v f u n c ( c o n s t s t d : : v e c t o r < d o u b l e > & x , s t d : : v e c t o r < d o u b l e > & g r a d , v o i d * m y _ f u n c _ d a t a )

{

i f ( ! g r a d . e m p t y ( ) ) {

g r a d [ 0 ] = 0 . 0 ;

g r a d [ 1 ] = 0 . 5 / s q r t ( x [ 1 ] ) ;

}

r e t u r n s q r t ( x [ 1 ] ) ;

}

d o u b l e m y v c o n s t r a i n t ( c o n s t s t d : : v e c t o r < d o u b l e > & x , s t d : : v e c t o r < d o u b l e > & g r a d , v o i d * d a t a )

{

m y _ c o n s t r a i n t _ d a t a * d = r e i n t e r p r e t _ c a s t < m y _ c o n s t r a i n t _ d a t a * > ( d a t a ) ;

d o u b l e a = d - > a , b = d - > b ;

i f ( ! g r a d . e m p t y ( ) ) {

g r a d [ 0 ] = 3 * a * ( a * x [ 0 ] + b ) * ( a * x [ 0 ] + b ) ;

g r a d [ 1 ] = - 1 . 0 ;

}

r e t u r n ( ( a * x [ 0 ] + b ) * ( a * x [ 0 ] + b ) * ( a * x [ 0 ] + b ) - x [ 1 ] ) ;

}

Notice that, instead of checking whether g r a d is N U L L , we check whether it is empty. (The vector arguments, ifnon-empty, are guaranteed to be of the same size as the dimension of the problem that you specified.) We thenspecify these in the same way as before:

o p t . s e t _ m i n _ o b j e c t i v e ( m y v f u n c , N U L L ) ;

o p t . a d d _ i n e q u a l i t y _ c o n s t r a i n t ( m y v c o n s t r a i n t , & d a t a [ 0 ] , 1 e - 8 ) ;

o p t . a d d _ i n e q u a l i t y _ c o n s t r a i n t ( m y v c o n s t r a i n t , & d a t a [ 1 ] , 1 e - 8 ) ;

Note that the data pointers passed to these functions must remain valid (or rather, what they point to must remainvalid) until you are done with o p t . (It might have been nicer to use s h a r e d _ p t r , but I don't like to rely onbleeding-edge language features.)

Instead of passing a separate data pointer, some users may wish to define a C++ function object class that contains allof the data needed by their function, with an overloaded o p e r a t o r ( ) method to implement the function call. Youcan easily do this with a two-line helper function. If your function class is MyFunction, then you could define a staticmember function:

s t a t i c d o u b l e w r a p ( c o n s t s t d : : v e c t o r < d o u b l e > & x , s t d : : v e c t o r < d o u b l e > & g r a d , v o i d * d a t a ) {

r e t u r n ( * r e i n t e r p r e t _ c a s t < M y F u n c t i o n * > ( d a t a ) ) ( x , g r a d ) ; }

which you would then use e.g. by o p t . s e t _ m i n _ o b j e c t i v e ( M y F u n c t i o n : : w r a p ,& s o m e _ M y F u n c t i o n ) . Again, you have to make sure that s o m e _ M y F u n c t i o n does not go out of scope beforeyou are done calling n l o p t : : o p t : : o p t i m i z e .

To link your program, just link to the C NLopt library (- l n l o p t - l m on Unix).

Example in Matlab or GNU Octave

To implement this objective function in Matlab (or GNU Octave), we would write a file myfunc.m that looks like:

f u n c t i o n [ v a l , g r a d i e n t ] = m y f u n c ( x )

v a l = s q r t ( x ( 2 ) ) ;

i f ( n a r g o u t > 1 )

g r a d i e n t = [ 0 , 0 . 5 / v a l ] ;

e n d

Notice that we check the Matlab builtin variable n a r g o u t (the number of output arguments) to decide whether tocompute the gradient. If we use a derivative-free optimization algorithm below, then n a r g o u t will always be 1 andthe gradient need never be computed.

Our constraint function looks similar, except that it is parameterized by the coefficients D and E. We can just add theseon as extra parameters, in a file m y c o n s t r a i n t . m :

f u n c t i o n [ v a l , g r a d i e n t ] = m y c o n s t r a i n t ( x , a , b )

v a l = ( a * x ( 1 ) + b ) ^ 3 - x ( 2 ) ;

i f ( n a r g o u t > 1 )

g r a d i e n t = [ 3 * a * ( a * x ( 1 ) + b ) ^ 2 , - 1 ] ;

e n d

The equivalent of the n l o p t _ o p t is just a structure(http://www.mathworks.com/access/helpdesk/help/techdoc/matlab_prog/f2-88951.html) , with fields corresponding toany parameters that we want to set. (Any structure fields that we don't include are equivalent to not setting thoseparameters, and using the defaults instead). You can get more information on the available parameters by typingh e l p n l o p t _ o p t i m i z e in Matlab. The equivalent of the C example above is to define an o p t structure by:

o p t . a l g o r i t h m = N L O P T _ L D _ M M A

o p t . l o w e r _ b o u n d s = [ - i n f , 0 ]

o p t . m i n _ o b j e c t i v e = @ m y f u n c

o p t . f c = { ( @ ( x ) m y c o n s t r a i n t ( x , 2 , 0 ) ) , ( @ ( x ) m y c o n s t r a i n t ( x , - 1 , 1 ) ) }

o p t . f c _ t o l = [ 1 e - 8 , 1 e - 8 ] ;

o p t . x t o l _ r e l = 1 e - 4

We do not need to specify the dimension of the problem; this is implicitly specified by the size of the initial-guessvector passed to n l o p t _ o p t i m i z e below (and must match the sizes of other vectors likeo p t . l o w e r _ b o u n d s ). The inequality constraints are specified as a cell array

(http://blogs.mathworks.com/loren/2006/06/21/cell-arrays-and-their-contents/) o p t . f c of function handles (and thecorresponding tolerances are in an array o p t . f c _ t o l ); notice how we use @ ( x ) to define an anonymous/inlinefunction in order to pass additional arguments to m y c o n s t r a i n t .

Finally, we call n l o p t _ o p t i m i z e :

[ x o p t , f m i n , r e t c o d e ] = n l o p t _ o p t i m i z e ( o p t , [ 1 . 2 3 4 5 . 6 7 8 ] )

n l o p t _ o p t i m i z e returns three things: x o p t , the optimal parameters found; f m i n , the corresponding value of theobjective function, and a return code r e t c o d e (positive on success and negative on failure).

The output of the above command is:

x o p t =

0 . 3 3 3 3 0 . 2 9 6 3

f m i n = 0 . 5 4 4 3

r e t c o d e = 4

(The return code 4 corresponds to N L O P T _ X T O L _ R E A C H E D , which means it converged to the specified [tolerance.) To switch to a derivative-free algorithm like COBYLA, we just change o p t . a l g o r i t h m parameter:

o p t . a l g o r i t h m = N L O P T _ L N _ C O B Y L A

Matlab verbose output

It is often useful to print out some status message to see what is happening, especially if your function evaluation ismuch slower or if a large number of evaluations are required (e.g. for global optimization). You can, of course, modifyyour function to print out whatever you want. As a shortcut, however, you can set a verbose option in NLopt's Matlabinterface by:

o p t . v e r b o s e = 1 ;

If we do this, then running the MMA algorithm as above yields:

n l o p t _ m i n i m i z e _ c o n s t r a i n e d e v a l # 1 : 2 . 3 8 2 8 6



n l o p t _ m i n i m i z e _ c o n s t r a i n e d e v a l # 4 : 2 . 0 1 9 1



n l o p t _ m i n i m i z e _ c o n s t r a i n e d e v a l # 7 : 1 . 0 2 2 3

n l o p t _ m i n i m i z e _ c o n s t r a i n e d e v a l # 8 : 0 . 6 8 5 2 0 3

n l o p t _ m i n i m i z e _ c o n s t r a i n e d e v a l # 9 : 0 . 5 5 2 9 8 5

n l o p t _ m i n i m i z e _ c o n s t r a i n e d e v a l # 1 0 : 0 . 5 4 4 3 5 4

n l o p t _ m i n i m i z e _ c o n s t r a i n e d e v a l # 1 1 : 0 . 5 4 4 3 3 1

This shows the objective function values at each intermediate step of the optimization. As in the C example above, itconverges in 11 steps. The COBYLA algorithm requires a few more iterations, because it doesn't exploit the gradientinformation:

n l o p t _ o p t i m i z e e v a l # 1 : 2 . 3 8 2 8 6




n l o p t _ o p t i m i z e e v a l # 5 : 0 . 4 9 9 4 4 1





n l o p t _ o p t i m i z e e v a l # 1 0 : 0 . 3 2 4 6 7 9






















Notice that some of the objective function values are below the minimum of 0.54433 — these are simply values of theobjective function at infeasible points (violating the nonlinear constraints).

Example in Python

The same example in Python is:

i m p o r t n l o p t

f r o m n u m p y i m p o r t *

d e f m y f u n c ( x , g r a d ) :

i f g r a d . s i z e > 0 :

g r a d [ 0 ] = 0 . 0

g r a d [ 1 ] = 0 . 5 / s q r t ( x [ 1 ] )

r e t u r n s q r t ( x [ 1 ] )

d e f m y c o n s t r a i n t ( x , g r a d , a , b ) :

i f g r a d . s i z e > 0 :

g r a d [ 0 ] = 3 * a * ( a * x [ 0 ] + b ) * * 2

g r a d [ 1 ] = - 1 . 0

r e t u r n ( a * x [ 0 ] + b ) * * 3 - x [ 1 ]

o p t = n l o p t . o p t ( n l o p t . L D _ M M A , 2 )

o p t . s e t _ l o w e r _ b o u n d s ( [ - f l o a t ( ' i n f ' ) , 0 ] )

o p t . s e t _ m i n _ o b j e c t i v e ( m y f u n c )

o p t . a d d _ i n e q u a l i t y _ c o n s t r a i n t ( l a m b d a x , g r a d : m y c o n s t r a i n t ( x , g r a d , 2 , 0 ) , 1 e - 8 )

o p t . a d d _ i n e q u a l i t y _ c o n s t r a i n t ( l a m b d a x , g r a d : m y c o n s t r a i n t ( x , g r a d , - 1 , 1 ) , 1 e - 8 )

o p t . s e t _ x t o l _ r e l ( 1 e - 4 )

x = o p t . o p t i m i z e ( [ 1 . 2 3 4 , 5 . 6 7 8 ] )

m i n f = o p t . l a s t _ o p t i m u m _ v a l u e ( )

p r i n t " o p t i m u m a t " , x [ 0 ] , x [ 1 ]

p r i n t " m i n i m u m v a l u e = " , m i n f

p r i n t " r e s u l t c o d e = " , o p t . l a s t _ o p t i m i z e _ r e s u l t ( )

Notice that the o p t i m i z e method returns only the location of the optimum (as a NumPy array), and that the valueof the optimum and the result code are obtained by l a s t _ o p t i m u m _ v a l u e and l a s t _ o p t i m i z e _ r e s u l tvalues. Like in C++, the NLopt functions raise exceptions on errors, so we don't need to check return codes to lookfor errors.

The objective and constraint functions take NumPy arrays as arguments; if the g r a d argument is non-empty it mustbe modified in-place to the value of the gradient. Notice how we use Python's l a m b d a construct to pass additionalparameters to the constraints. Alternatively, we could define the objective/constraints as classes with a_ _ c a l l _ _ ( s e l f , x , g r a d ) method so that they can behave like functions.

The result of running the above code should be:

o p t i m u m a t 0 . 3 3 3 3 3 3 3 3 1 3 6 6 0 . 2 9 6 2 9 6 2 9 2 6 9 7

m i n i m u m v a l u e = 0 . 5 4 4 3 3 1 0 5 0 6 4 6

r e s u l t = 4

finding the same correct optimum as in the C interface (of course). (The return code 4 corresponds ton l o p t . X T O L _ R E A C H E D , which means it converged to the specified x tolerance.)

Important: Modifying g r a d in-place

The grad argument of your objective/constraint functions must be modified in-place. If you use an operation like

g r a d = 2 * x

however, Python allocates a new array to hold 2 * x and reassigns grad to point to it, rather than modifying the originalcontents of grad. This will not work. Instead, you should do:

g r a d [ : ] = 2 * x

which overwrites the old contents of grad with 2 * x . See also the NLopt Python Reference.

Example in GNU Guile (Scheme)

In GNU Guile, which is an implementation of the Scheme programming language, the equivalent of the example abovewould be:

( u s e - m o d u l e s ( n l o p t ) )

( d e f i n e ( m y f u n c x g r a d )

( i f g r a d

( b e g i n

( v e c t o r - s e t ! g r a d 0 0 . 0 )

( v e c t o r - s e t ! g r a d 1 ( / 0 . 5 ( s q r t ( v e c t o r - r e f x 1 ) ) ) ) ) )

( s q r t ( v e c t o r - r e f x 1 ) ) )

( d e f i n e ( m y c o n s t r a i n t x g r a d a b )

( l e t ( ( x 0 ( v e c t o r - r e f x 0 ) ) ( x 1 ( v e c t o r - r e f x 1 ) ) )

( i f g r a d

( b e g i n

( v e c t o r - s e t ! g r a d 0 ( * 3 a ( e x p t ( + ( * a x 0 ) b ) 2 ) ) )

( v e c t o r - s e t ! g r a d 1 - 1 . 0 ) ) )

( - ( e x p t ( + ( * a x 0 ) b ) 3 ) x 1 ) ) )

( d e f i n e o p t ( n e w - n l o p t - o p t N L O P T - L D - M M A 2 ) )

( n l o p t - o p t - s e t - l o w e r - b o u n d s o p t ( v e c t o r ( - ( i n f ) ) 0 ) )

( n l o p t - o p t - s e t - m i n - o b j e c t i v e o p t m y f u n c )

( n l o p t - o p t - a d d - i n e q u a l i t y - c o n s t r a i n t o p t ( l a m b d a ( x g r a d )

( m y c o n s t r a i n t x g r a d 2 0 ) )

1 e - 8 )

( n l o p t - o p t - a d d - i n e q u a l i t y - c o n s t r a i n t o p t ( l a m b d a ( x g r a d )

( m y c o n s t r a i n t x g r a d - 1 1 ) )

1 e - 8 )

( n l o p t - o p t - s e t - x t o l - r e l o p t 1 e - 4 )

( d e f i n e x ( n l o p t - o p t - o p t i m i z e o p t ( v e c t o r 1 . 2 3 4 5 . 6 7 8 ) ) )

( d e f i n e m i n f ( n l o p t - o p t - l a s t - o p t i m u m - v a l u e o p t ) )

( d e f i n e r e s u l t ( n l o p t - o p t - l a s t - o p t i m i z e - r e s u l t o p t ) )

Note that the objective/constraint functions take two arguments, x and g r a d , and return a number. x is a vectorwhose length is the dimension of the problem; grad is either false (# f ) if it is not needed, or a v e c t o r that must bemodified in-place to the gradient of the function.

On error conditions, the NLopt functions throw exceptions(http://www.gnu.org/software/guile/manual/html_node/Exceptions.html) that can be caught by your Scheme code ifyou wish.

The heavy use of side-effects here is a bit unnatural in Scheme, but is used in order to closely map to the C++interface. (Notice that n l o p t : : C++ functions map to n l o p t - Guile functions, and n l o p t : : o p t : : methodsmap to n l o p t - o p t - functions that take the o p t object as the first argument.) Of course, you are free to wrap yourown Scheme-like functional interface around this if you wish.

Example in Fortran

In Fortran, the equivalent of the C example above would be as follows. First, we would write our functions as:

s u b r o u t i n e m y f u n c ( v a l , n , x , g r a d , n e e d _ g r a d i e n t , f _ d a t a )

d o u b l e p r e c i s i o n v a l , x ( n ) , g r a d ( n )

i n t e g e r n , n e e d _ g r a d i e n t

i f ( n e e d _ g r a d i e n t . n e . 0 ) t h e n

g r a d ( 1 ) = 0 . 0

g r a d ( 2 ) = 0 . 5 / d s q r t ( x ( 2 ) )

e n d i f

v a l = d s q r t ( x ( 2 ) )

e n d

s u b r o u t i n e m y c o n s t r a i n t ( v a l , n , x , g r a d , n e e d _ g r a d i e n t , d )

i n t e g e r n e e d _ g r a d i e n t

d o u b l e p r e c i s i o n v a l , x ( n ) , g r a d ( n ) , d ( 2 ) , a , b

a = d ( 1 )

b = d ( 2 )

i f ( n e e d _ g r a d i e n t . n e . 0 ) t h e n

g r a d ( 1 ) = 3 . * a * ( a * x ( 1 ) + b ) * * 2

g r a d ( 2 ) = - 1 . 0

e n d i f

v a l = ( a * x ( 1 ) + b ) * * 3 - x ( 2 )

e n d

Notice that that the "functions" are actually subroutines. This is because it turns out to be hard to call Fortran functionsfrom C or vice versa in any remotely portable way. Therefore:

In the NLopt Fortran interface, all C functions become subroutines in Fortran, with the return value becomingthe first argument.

So, here the first argument v a l is used for the return value. Also, because there is no way in Fortran to pass N U L Lfor the g r a d argument, we add an additional n e e d _ g r a d i e n t argument which is nonzero if the gradient needs tobe computed. Finally, the last argument is the equivalent of the v o i d * argument in the C API, and can be used topass a single argument of any type through to the objective/constraint functions: here, we use it in m y c o n s t r a i n tto pass an array of two values for the constants D and E.

Then, to run the optimization, we can use the following Fortran program:

p r o g r a m m a i n

e x t e r n a l m y f u n c , m y c o n s t r a i n t

d o u b l e p r e c i s i o n l b ( 2 )

i n t e g e r * 8 o p t

d o u b l e p r e c i s i o n d 1 ( 2 ) , d 2 ( 2 )

d o u b l e p r e c i s i o n x ( 2 ) , m i n f

i n t e g e r i r e s

i n c l u d e ' n l o p t . f '

c a l l n l o _ c r e a t e ( o p t , N L O P T _ L D _ M M A , 2 )

c a l l n l o _ g e t _ l o w e r _ b o u n d s ( i r e s , o p t , l b )

l b ( 2 ) = 0 . 0

c a l l n l o _ s e t _ l o w e r _ b o u n d s ( i r e s , o p t , l b )

c a l l n l o _ s e t _ m i n _ o b j e c t i v e ( i r e s , o p t , m y f u n c , 0 )

d 1 ( 1 ) = 2 .

d 1 ( 2 ) = 0 .

c a l l n l o _ a d d _ i n e q u a l i t y _ c o n s t r a i n t ( i r e s , o p t ,

$ m y c o n s t r a i n t , d 1 , 1 . D - 8 )

d 2 ( 1 ) = - 1 .

d 2 ( 2 ) = 1 .

c a l l n l o _ a d d _ i n e q u a l i t y _ c o n s t r a i n t ( i r e s , o p t ,

$ m y c o n s t r a i n t , d 2 , 1 . D - 8 )

c a l l n l o _ s e t _ x t o l _ r e l ( i r e s , o p t , 1 . D - 4 )

x ( 1 ) = 1 . 2 3 4

x ( 2 ) = 5 . 6 7 8

c a l l n l o _ o p t i m i z e ( i r e s , o p t , x , m i n f )

i f ( i r e s . l t . 0 ) t h e n

w r i t e ( * , * ) ' n l o p t f a i l e d ! '

e l s e

w r i t e ( * , * ) ' f o u n d m i n a t ' , x ( 1 ) , x ( 2 )

w r i t e ( * , * ) ' m i n v a l = ' , m i n f

e n d i f

c a l l n l o _ d e s t r o y ( o p t )

e n d

There are a few things to note here:

All n l o p t _ functions are converted into n l o _ subroutines, with return values converted into the firstargument.The "n l o p t _ o p t " variable o p t is declared as i n t e g e r * 8 . (Technically, we could use any type that is bigenough to hold a pointer on all platforms; i n t e g e r * 8 is big enough for pointers on both 32-bit and 64-bit

machines.)The subroutines must be declared as e x t e r n a l .We i n c l u d e ' n l o p t . f ' in order to get the various constants like N L O P T _ L D _ M M A .

There is no standard Fortran 77 equivalent of C's H U G E _ V A L constant, so instead we just calln l o _ g e t _ l o w e r _ b o u n d s to get the default lower bounds (-∞) and then change one of them. In Fortran 90 (andsupported as an extension in many Fortran 77 compilers), there is a h u g e intrinsic function that we could have usedinstead:

l b ( 1 ) = - h u g e ( l b ( 1 ) )

Retrieved from "http://ab-initio.mit.edu/wiki/index.php/NLopt_Tutorial"

Category: NLopt

This page was last modified 17:16, 16 July 2010.

This page has been accessed 26,599 times.Privacy policy

About AbInitioDisclaimers

NLopt Tutorial - AbInitio

Documents

means local optimization

free optimization algorithm

dbe ecii

additional data

dimension oi

ca add ieai cai

inequality constraints

nonlinear constraints