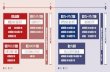
Input Function x(t) Output Function y(t) T[ ]. Consider The following Input/Output relations.

SystemInput Signal Output Signal

- A collection of items that together performs a function - Modifies / transforms an input to give an output

System

Represented by

Input Function x(t)

Output Function y(t)

T[ ]

Consider The following Input/Output relations

i(t)

RRV ( )t

RV ( ) ( )t Ri t

i(t)

C CV ( )t

C

1V ( ) ( )

t

t i dC

i(t)

L LV ( )t

L( )

V ( )di t

t Ldt

In general we can represent the simple relation between the input and output as:

x( )t

Input

y( )t

Output y(t) = T[ x(t) ]

Were T[ ] is an operator that map the function x(t) to another function y(t) .( Function to Function mapping)

T[ ]

Example

Let the input x(t) = 2sin(4pt) then the output y(t) be

T[ ] = d [ ]dt

Let the operator Differential Operator

T[x(y(t) = t)] = 2sin(4d [ ]dt

)t = 8cos(4 )t

Function 2sin(4pt) mapped Function 8cos(4pt)

( ) ( )x t Ri V tc

C

R

( )x t

( )i t

( )V tC

( )( )

dV tci t Cdt

( )

( ) ( )dV tcx t RC V tcdt

Input Input

Output

The operator or relation T can be defined as

- Linear / Non linear

- Time Invariant / Time Variant

- Continuous-Time / Discrete-Time

- Causal / Non Causal

Representation of a general system

y(t) = T[x(t)]

where the notation T[x(t)] indicates a transformation or mapping

This notation T[.] does not indicate a function

that is, T[x(t)] is not a mathematical function into which we substitutex(t) and directly calculate y(t).

The explicit set of equations relating the input x(t) and the output y(t) is called the mathematical model, or simply, the model, of the system

Properties of Continuous Time Systems

( )x t[ ]S

( ) [ ( )]y t S x ttime shift

( )oy t t

( )x t[ ]S

[ ( )]oS x t ttime shift

( )ox t t

( )i t[ ]S time shift

( ) [ ( )]C

V t S i t 1 ( )t

i dC

1( ) ( )

o

C

t t

oV t t i dC

time shift

( )i t ( )oi t t[ ]S

1[ ( )] ( )t

o oS i t t i t dC

1The capacitor is time-invariant if [ ( )] ( ) ( )C

t

o o oS i t t V t t i t dC

1 1( ) ( )

ot tt

oi t d i dC C

OR

1Is the capacitor is time-invariant ? ( ) ( )C

t

V t i dC

both output of the block diagram are equal

both output of the block diagram are equal The capacitor is time-invariant

are equal

The resistor is time-invariant

are not equal

is time-variant

Is ( ) = ( ) time-invariant ?t

z t x d

let = ot [ ( )]= ( )ot t

oS x t t x d

( )oz t t time-invariant

are they equal ?

0

Is ( ) = ( ) time-invariant ?t

z t x d

let = ot [ ( )]= ( )o

o

t t

ot

S x t t x d

time-variant

are they equal ?

0

( ) = ( )t

oz t t x d

0

[ ( )] = ( )t

o oS x t t x t d

( )oz t t 0

( )t

x d

Examples of Linear systems

1 2[ ( ) ( )]c ax t bx t 1 2( ) ( )cax t cbx t 1 2( ) ( )cy t cy t

Examples of Nonlinear systems

We can stop here and imply the system is non linear

violates Additivity due to the cross terms

To satisfy homogeneity [ ( )] ( ) ( )S cx t cy t cx t ca

( )cx t ca

We can stop here and imply the system is non linear

1( )x t

[ ]S

To check additivity

1 1[ ( )] = ( )S x t x t a

2( )x t 2 2[ ( )] = ( )S x t x t a

1 2( ) ( )x t x t 1 2 1 2[ ( ) ( )] = ( ) ( )S x t x t x t x t a

1 2[ ( )]+ [ ( )]S x t S x t

( )x t ( )y tx(t)H[ ]

( ) ( )x dt

H

Linear –Time Invariant

( ) ( )y(t) = H x dt

Operator with respect to t Integration with respect to l

( ) ( )H= x t d

constant with respect to t

( ) ( )H= x t d

() )(= h t dx

( )t( )h t(t)H[ ]

The convolution integral

Evaluate ( ) ( ) h x t d

Moving

Fix

Example 2-7

( )h

Sep 1 : make the functions or signals in terms of the variable l

( )x

)( ()xh t d

Sep 2 : make the moving function in terms of l

6t 4t

Sep 2 : add t to to form ( t )

t t

( )x t

Moving to the right

( )h

For t ≤ 4 there is no overlapping between the functions

6t 4t

( )x t

( )( ) 0dx th

4 6

4

0

(1)(2)

t

d

4

02

t 2(( 4) 0)t 2 8t

t0

4

4

6

(1)(2)

t

t

d

4

62

t

t

2(( 4) ( 6))t t 4

4 6t

0

4

8

4

6

(1)(2)t

d 4

62

t

2((4) ( 6))t 2 20t

4 6t

0

4

8 10

( )h

For t ≥ 10

6t 4t

( )x t

( )( ) 0dx th

For t ≥ 10 there is no overlapping between the functions

4 6t

0

4

8 10

)( ()xh t d

t

Since | ( ) | | ( ) |h d d

0

|1| d

( ) ( ) not stableh t u t

0 0

10

1

( ) cos sinnn

n n

x t n ta a b n t

0

0

0

1 ( )T

x t dtT

a The average of x(t)

0

00

cos2 ( ) 0n

T

a n tx t dt nT

00

0sin2 ( )n

T

b nx t dt tT

Chapter 3 The Fourier Series0jn t

n

nX e

0

00

1 ( ) jn t

T

n x t e dtT

X

| |k kkC C

| |kC

10

0 1 2 3

1.52.5

2.01.52.5

2.0

123 k

10

0 1 2

3

12

3 k

30o

30o

90o

90o

k

since ( ) is an odd function 0o

x t C

kC

Time domain Fourier domain or Frequency domain

one to one

Let ( ) = ( ) + y t Ax t B

Known

0

kyjk t

k

C e

unknown

what are the coefficients interms of the coefficientsky kxC CQuestion unknown known

Writing y(t) as

0

y

C

ky

C

0 0y xC AC B 0

ky kxC AC k

Let ( ) be as shownx t

Let ( ) = ( ) + y t Ax t B

Let ( ) be as showny t

one to one

one to onewhat are and

oy kyC C

0( ) kyjk t

k

Cy t e

unknown

We wish to find the Fourier series for the sawtooth signal ( ) y t

First, note that the total amplitude variation of ( ) is while the total variation of ( ) is 4. x t X y to4Also note that we invert x(t) to get y(t), yielding =

o

AX

4 ( ) = ( ) + ( ) + 1o

y t Ax t B x tX

one to one

one to onewhat are and

oy kyC C

0( ) kyjk t

k

Cy t e

unknown

4 ( ) = ( ) + ( ) + 1o

y t Ax t B x tX

( ) ( ) j tx t X e d

1( ) ( )2

j tX x t e dt

Fourier Transform Pairs

Sufficient conditions for the existence of the Fourier transform are

On any finite interval, a. ( ) is bounded; b. ( ) has a finite number of maxima

f tf t

( Dirichlet conditions )

1.

and minima; and c. ( ) has a finite number of discontinuities.

f (t) is absolutely integrable; that is, ( )

Note that these are conditions and not condi

f t

f t dt

2.

sufficient necessary tions

you can have a function that is not absolutely integrable however it has Fourier Transform like cos( ) (will be shown later)tNote

0)()( atuetx at

( )

0( ) ( )at j t a j tX j e u t e dt e dt

Finding the Fourier Transform

1a

( )

0

1

( )a j te

a j

1

( )a j

0)()( atuetx at 1( )

( )X j

a j

0)()( atuetx at 1( )

( )X j

a j

Example Find the Fourier Transform for the following function

aa( ) ( ) j tX x t e dt

1

1

j te dt

1

1

j tej

2sinc( )

j je ej

22

j je ej

2 sin( )

sin( )2

(1) ( 1)j je ej

a ( ) 2sinc( )X

2

a( )X

22

a ( ) 2sinc( )X

aa

( )| ( )|( ) jXX e

2

0

a| ( )|X

22

0

( )f

2 2

2

a( )X

22

Example

0

b( )x t

t1 1

1

1bb( ) ( ) j tX x t e dt

0 1

1 0

(1) ( 1) j t te dt e dt

2sinc

2j

bb

( )| ( )|( ) jXX e

b2sin| |

2) c(X

0

b( )x t

t1 1

1

1

2b ( ) sinc

2X f j

2

f0

( )f

2

2

2b ( ) sinc

2X j

bb

( )| ( )|( ) jXX e

oAlways 0  it add no angle (0 )

( )t 1

1 21 1 1 1 1 2[ ( ) ( ) ] ( ) + ( )F a x t a x t a X a X 1-Linearity

Properties of the Fourier Transform

( )X 1( )X 2( )X

(1)(4)sinc(4 ) (2)(2)sinc(2 ) +

( )sinc( )A T T

4sinc(4 ) 4sinc(2 )+

Using Fourier Transform Properties

Let ( ) ( )x t X Then1( ) ta

aax X

2-Time-Scaling (compressing or expanding)

) 2sinc( )(aX

2(2sinc(2 ))

what is the fourier transform of

Let

11

21 2 ( ) aX X

since ( )1 2

a

tx t x

2 2 )(aX

4sinc(2 )

00 Let ( ) Then ( ) ( ) ( )e tjx t x t tX X

3-Time-Shifting

Example Find the Fourier Transform of the pulse function

0

( )x t

t2

1

Solution

From previous Example

a ( ) 2sin (2 )X c

Since ( ) ( )1ax t x t 1( )

2sinc(2 ) = e j

2sinc(2 ) = e j

0 ( ) ( )e a

tjX X

If ( ) ( ) ( ) 2 ) (Xx t tX x then

2W

2W

2W

t

2 sinc(2 ) W Wt

Find the   of 2 sinc(2 ) W WtF.T

5-Duality ازدواجية

2W

2W

2W

t

12 sinc(2 ) ( ) ( 4 )2

W Wt X t W

2

sinc2

( ) = X

2

Step 1 from Known transform from the F.T Table

Step 2

t

2

0

1

t

( ) = rectt

x t

2

2W0

1

rect4W

2W

rect4W

Even Function

( ) 2 ( )tX x

1 ( ) ( )2

2 x x

2 21 1( ) ( ) ( ( ) )x t x t X X

6- The convolution Theorem

2 21 11( ) ( ) ) ( )

2( Xx t x t X

The multiplication Theorem

rect rectt t

Find the Fourier Transform of following

Solution

Since rect

t

t

2

2 0

rect

t

t

2

2 0

trit

t 0

convolution

Time

sinc( )f sinc( )f 2 2sinc ( )f Frequencymultiplication

System Analysis with Fourier Transform

= ( ) ( ) x h t d

( )x t

( )h ty(t) = ( ( ) )x t h t

( )X ( )H ( )Y ( ) ( )X H

( ) ) ) ( (Y X H y(t) = ( ( ) )x t h t

convolution in time

multiplication in Frequency

impulse response

convolution in timemultiplication in Frequency

7-Differentiation

Let ( ) ( ) ( ) ( )( ) d

dtx t x t j XX

1( ) ( ) (0) ( )t

x d X Xj

7- Integration

? 0

( ) ( ) j tF f t e dt

0

( )k

Find the Transfer Function for the following RC circuit

C

R

( )x t

( )y t

( ) ( ) ( ) dy tRC y t x t t

dt

C

R

( )t

( )h t

( ) ( ) ( )dh tRC h t t

dt

1( ) ( )t

R Ch t e u tR C

we can find h(t) by solving differential equation as follows

Method 1

C

R

( )x t

( )y t

( ) ( ) ( )dy tRC y t x t

dt

( )FT ( ) FT ( ) dy tRC y t x t

dt

( ) ( ) ( ) ( ) RC j Y Y X

( ) 1 ( ) ( ) j RC Y X

( )( )

( ) Y

HX

1( ) 1j RC

We will find h(t) using Fourier Transform Method rather than solving differential equation as follows

Method 2

C

R

( )x t

( )y t

( ) ( ) ( )dy tRC y t x t

dt

( )( )

( ) Y

HX

1( ) 1j RC

(1/ )( ) (1/ )

RCj RC

1( ) ( ) > 0 tx t e u tj

1( ) ( )t

R Ch t e u tR C

From Table 4-2

C

R

( )x t

( )y t

Method 3

R

( )X

( )Y

1j C

Fourier Transform

1

( ) ( )1

j CY f X

Rj C

1( )

1X

j RC

( ) 1( )

( ) 1

YH

X j RC

1( ) ( )t

R Ch t e u tR C

C

R

( )x t

( )y t

R

( )X

( )Y

1j C

Fourier Transform

( ) 1( )

( ) 1

YH

X j RC

2

1| ( ) |

1 ( )H

RC

( )H | ( ) |H

( )H 1tan ( )RC

2

1| ( ) |

1 ( )H

RC

( )H 1tan ( )RC

1( )

1H

j RC

C

R

( )x t

( )y t

Find y(t) if the input x(t) is

( ) ( )tx t A e u t

Method 1 ( convolution method)

Using the time domain ( convolution method , Chapter 3)

y( ) = ( ) ) (t x t h t

1( ) ( )t

R Ch t e u tR C

Example

C

R

( )x t

( )y t

( ) ( )tx t A e u t

/ ( )(1/ )

A RCj RC j

1 1( ) 1/1AY jRC jRC

Using partial fraction expansion (will be shown later)

From Table 5-2 /( ) ( )1

t RC tAy t e e u tRC

( ) AXj

1( ) ( )t

R Ch t e u tR C

(1/ )( )

(1/ ) ( )RCH

RC j

( ) ) ( ( )Y X H

Method 2 Fourier Transform

Sine Y(w) is not on the Fourier Transform Table 5-2