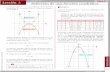
unción Cuadrática y unción Cuadrática y Ecuación de Segundo G rado cuación de Segundo Grado Prof. Isaías Correa M. Prof. Isaías Correa M.

Welcome message from author
This document is posted to help you gain knowledge. Please leave a comment to let me know what you think about it! Share it to your friends and learn new things together.
Transcript
-
Funcin Cuadrtica y Ecuacin de Segundo GradoProf. Isaas Correa M.
-
OBJETIVOS:Conocer y aplicar los conceptos matemticos asociados al estudio de la funcin cuadrtica.Graficar una funcin cuadrtica, determinando vrtice, eje de simetra y concavidad.Indicar las caractersticas grficas de una parbola a travs del anlisis del discriminante.Determinar las intersecciones de la parbola con los ejes cartesianos.Determinar las races de una ecuacin de 2 grado.
-
ContenidosFuncin cuadrtica2.Ecuacin de 2 grado1.1 Interseccin con el eje Y1.2 Concavidad 1.3 Eje de simetra y vrtice2.1 Races de una ecuacin cuadrtica2.2 Propiedades de las races2.3 Discriminante1.4 Discriminante
-
1. Funcin Cuadrtica Es de la forma: f(x) = ax2 + bx + cEjemplos: y su grfica es una parbola.a) Si f(x) = 2x2 + 3x + 1b) Si f(x) = 4x2 - 5x - 2a = 2, b = 3 y c = 1a = 4, b = -5 y c = -2
-
1.1. Interseccin con eje YEn la funcin cuadrtica, f(x) = ax2 + bx + c , el coeficiente c indica la ordenada del punto donde la parbola intersecta al eje Y.
-
1.2. ConcavidadEn la funcin cuadrtica, f(x) = ax2 + bx + c , el coeficiente a indica si la parbola es cncava hacia arriba o hacia abajo.Si a > 0,es cncava hacia arribaSi a < 0,es cncava hacia abajo
-
Luego, la parbola intersecta al eje Y en el punto (0,- 4) y es cncava hacia arriba.Ejemplo:En la funcin f(x) = x2 - 3x - 4 , a = 1 y c = - 4.
- El valor de b en la ecuacin permite saber el movimientohorizontal de la parbola y a su concavidad. Sea la funcin cuadrtica f(x)=ax +bx + cEntonces:Si a>0 y b0 y b>0 la parbola abre hacia arriba y est orientada hacia la izquierda. Si a0 la parbola abre hacia abajo y esta orientada hacia la derecha.Si a
-
1.4. Eje de simetra y vrticeEl eje de simetra es la recta que pasa por el vrtice de la parbola, y es paralela al eje Y.Eje de simetraVrticeEl vrtice de una parbola es el punto ms alto o ms bajo de la curva, segn sea su concavidad.
-
Si f(x) = ax2 + bx + c , entonces: b) Su vrtice es:a) Su eje de simetra es:
-
Ejemplo:En la funcin f(x) = x2 + 2x - 8, a = 1, b = 2 y c = - 8, entonces:V = ( -1, f(-1) )a) Su eje de simetra es:x = -1b) Su vrtice es:V = ( -1, -9 )
-
f(x)V = ( -1, -9 )x = -1Eje de simetra:Vrtice:
-
y =a(x-h) Significa que la funcin se movi a la izquierda o derecha, h unidades y abre hacia arriba o hacia abajo.
Ej. 1) y=2(x-3) () 2) y=-3(x-4) ()
Si y=ax una funcin cuadrtica cualquiera, entonces:ii) y =a(x+h) significa que la funcin se movi a la izquierda o derecha, h unidades y abre hacia arriba o abajo.
Ej. 1) y= 4(x+2) () 2) y=-(x+1) ()1.5 Comportamiento de la funcin de acuerdo a a, h y k
-
iii) y=a(x-h) k significa que la funcin se movi a la derecha o izquierda y k unidades hacia arriba o hacia abajo.
Ej. 1) y=5(x-1) - 4 () 2) y=-3(x-7) + 6 ()iv) y=a(x + h) k significa que la funcin se movi a la derecha o izquierda y k unidades hacia arriba o hacia abajo.
Ej. 1) y=(x+6) - 5 () 2) y=-5(x+3) + 3 ()Obs. V(h,k) es el vrtice de la parbola.
-
Si la parbola es abierta hacia arriba, el vrtice es un mnimo y si la parbola es abierta hacia abajo, el vrtice es un mximo.
-
El discriminante se define como:a) Si el discriminante es positivo, entonces la parbola intersecta en dos puntos al eje X. > 0 1.6. Discriminante
-
b) Si el discriminante es negativo, entonces la parbola NO intersecta al eje X. < 0
-
c) Si el discriminante es igual a cero, entonces la parbola intersecta en un solo punto al eje X, es tangente a l. = 0
-
x2x12. Ecuacin de segundo gradoUna ecuacin cuadrtica o de segundo grado es de la forma: ax2 + bx + c = 0, con a 0Toda ecuacin de segundo grado tiene 2 soluciones o races. Si stas son reales, corresponden a los puntos de interseccin de la parbola f(x) = ax2 + bx + c con el eje X.
-
x2x1Ejemplo:En la funcin f(x) = x2 - 3x - 4 , la ecuacin asociada: x2 - 3x - 4 = 0 , tiene races -1 y 4. Luego, la parbola intersecta al eje X en esos puntos.
-
2.1. Races de una ecuacin de 2 gradoFrmula para determinar las soluciones (races) de una ecuacin de segundo grado: Ejemplo:Determinar las races de la ecuacin: x2 - 3x - 4 = 0
-
x1 = 4x2 = -1Tambin se puede obtener las races de la ecuacin factorizando como producto de binomios:x2 - 3x - 4 = 0(x - 4)(x + 1) = 0(x - 4)= 0 (x + 1)= 0x1 = 4x2 = -1
-
2.2. Propiedades de las racesSi x1 y x2 son las races de una ecuacin de segundo grado de la forma ax2 + bx + c = 0, entonces:1)2)3)Dadas las races o soluciones de una ecuacin de segundo grado, se puede determinar la ecuacin asociada a ellas.
a(x x1)(x x2) = 0
-
En una ecuacin de segundo grado, el discriminantea) Si el discriminante es positivo, entonces la ecuacin cuadrtica tiene dos soluciones reales x1, x2 y distintas.La parbola intersecta en dos puntos al eje X. > 0 2.3. Discriminantepermite conocer la naturaleza de las races.x1, x2 son reales y x1 x2x2x1
-
Si el discriminante es negativo, entonces la ecuacin cuadrtica no tiene solucin real.La parbola NO intersecta al eje X. < 0
-
c) Si el discriminante es igual a cero, entonces la ecuacin cuadrtica tiene dos races reales e iguales.La parbola intersecta en un solo punto al eje X. = 0x1, x2 son reales y x1 = x2x2x1=
Related Documents