Equation of Continuity - Union Collegeminerva.union.edu/labrakes/Fluids and Fluid Mechanics.pdfequation of continuity the volume of fluid in at point 1 equals the volume of fluid out

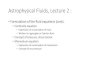
Fluids and Fluid Mechanics Fluids in motion – Dynamics Equation of Continuity

After having worked on fluids at rest we turn to a moving fluid. To describe a moving fluid we develop

two equations that govern the motion of the fluid through some medium, like a pipe. These two equations are the

equation of continuity (which says that the fluid flow rate is continuous) and the second is Bernoulli’s equation

(which is a statement of conservation of energy.) Consider the pipe in Figure #1 with varying cross-sectional area.

At point 1 let the cross-sectional area be A1 and at point 2 let the cross sectional area of the pipe be A2 . Fluid

enters point 1 from the left moving at velocity v1 . What we’d like to determine, is with what velocity will it leave

point 2. To do this we need to determine the mass flow rate is a constant throughout the pipe. That is, the mass of

fluid per unit time entering at point 1 and the mass of fluid per unit time leaving point 2. Providing that there are

no leaks in the system (the pipe) the mass of fluid entering the pipe at point 1 (per unit time) has to equal the mass

of fluid leaving the pipe at point 2 (per unit time.) To quantify this we write Δm1

Δt= Δm2

Δt. Thus we can write using

the density of the fluid, Δm1

Δt= ρ1ΔV1

Δt for the rate of change of the mass of fluid flowing past point 1 and similarly

Δm2

Δt= ρ2ΔV2

Δtfor the mass of fluid flowing past point 2. ΔV is the volume of fluid passing any point in space and

equating the two expressions gives Δm1

Δt= Δm2

Δt→ ρ1ΔV1

Δt= ρ2ΔV2

Δt→ ρ1A1Δl1

Δt= ρ2A2Δl2

Δt.

Figure #1: Diagram showing the relevant quantities used to determine the equation of continuity. D. Giancoli, Physics: Principles with Applications, 7th Ed., Prentice Hall.

The density of the fluid at point 1 and point 2 could be different allowing for the fact that the fluid may be

compressible. If the fluid is incompressible, as we will assume for everything that we will do, then ρ1 = ρ2 and we

identify ΔlΔt

= v as the speed of the fluid at any point. Therefore, we have ρ1A1Δl1Δt

= ρ2A2Δl2Δt

→ A1v1 = A2v2 , which

we call the equation of continuity. The equation of continuity gives us a way of determining the velocity of the

fluid moving at point 2. By the equitation of continuity, the amount of fluid moving past point 1 per unit time is

the same as that moving past point 2 per unit time. This implies that ρ1V1 = ρ2V2 and since the fluid is

incompressible the volume of fluid in (per unit time) at point 1 is equal to the volume of fluid out (per unit time) at

point 2. This is an alternate version of the equation of continuity and says the same thing.

Bernoulli’s Equation: Conservation of Energy in a Moving Fluid

Having the equation of continuity, we are now in a position to describe the moving fluid. Let’s assume that

we have a pipe as shown in Figure #2. The left end of the pipe at point 1 is at a height y1above the ground and the

fluid enters point 1 with a speed v1 through the pipe with cross-sectional area A1 . The fluid at point 2 leaves with a

speed v2 through a section of pipe with cross-sectional area A2 and point 2 is at a vertical height y2 above the

ground. We’d like, again, to determine the speed of the fluid when it leaves point 2. To do this we need to get the

fluid moving into point 1. This takes work and the work done to move the fluid into point 1 is given by some

applied force and how far into the pipe you need to move the mass of fluid. Thus, W1 = F1Δl1 = P1A1Δl1 , where P1 is

the pressure of the fluid at point 1 and Δl1 is the distance it takes to move a mass of fluid m1 past point 1. To keep

the fluid moving at point 2, we have to push on the fluid ahead of the incoming fluid that is moving toward point 2

from the left. The fluid immediately to the right of point 2 offers resistance against the incoming fluid. This takes

energy out of the fluid and costs work. The work done against the incoming fluid is W2 = −F2Δl2 = −P2A2Δl2 ,

where P2 is the pressure of the fluid at point 2 and Δl2 is the distance it takes to move a mass of fluid m2 past point

2. The net work done is equal to the change in energy of the system. Thus,

ΔEsystem =W1 +W2 = P1A1Δl1 − P2A2Δl2 = ΔKT + ΔKR + ΔUg + ΔUs . We assume that there is no change in spring

potential energy and that the fluid is not rotating.

Thus, we have ΔEsystem = P1A1Δl1 − P2A2Δl2 = ΔKT + ΔUg = 12 m2v2

2 − 12 m1v1

2( ) + m2gy2 −m1gy1( ) . Noting that is AΔl

the volume of the fluid at any point, we have P1V − P2V = 12 m2v2

2 − 12 m1v1

2( ) + m2gy2 −m1gy1( ) , where by the

equation of continuity the volume of fluid in at point 1 equals the volume of fluid out at point 2, namely

A1Δl1 = A2Δl2 →V1 =V2 =V . Now we divide both sides by the volume of fluid and note that the density of the

fluid is simply the ratio of the mass of the fluid divided by its volume. Further, we assume again that the fluid is

incompressible so that ρ1 = ρ2 = ρ . We have P1 − P2 = 12 ρv2

2 − 12 ρv1

2( ) + ρgy2 − ρgy1( ) , or

ΔE = 0 = P2 − P1( ) + 12 ρv2

2 − 12 ρv1

2( ) + ρgy2 − ρgy1( ) , in the absence of any external forces. This is called

Bernoulli’s equation and it’s a statement of conservation of energy in a moving fluid. The first term on the right is

the difference in pressure between points 1 and 2. The second term is the difference in the kinetic energy per unit

volume of fluid and the third is the difference in gravitational potential energy per unit volume of fluid. So, we

Figure #2: Diagram showing the relevant quantities used to determine the Bernoulli’s equation. D. Giancoli, Physics: Principles with Applications, 7th Ed., Prentice Hall.

identify the volume kinetic energy as KVolume

= 12 ρv

2 and the volume gravitational potential energy as

Ug

Volume= ρgy .

In fact, since Bernoulli’s equation is a statement of conservation of energy, it should apply to any situation.

How about a fluid at rest? Consider Figure #3 below in which the segment of fluid is at rest with respect to the

surrounding fluid. Thus v2 = v1 = 0 . The bottom of the cylinder of fluid is at a depth y2 below the surface while

the top of the cylinder is at depth y1below the surface, so that y2 − y1 = h . Therefore from Bernoulli’s equation the

pressure at the cylinder’s bottom P2 is:ΔE = 0 = P2 − P1( ) + ρgy2 − ρgy1( )→ P2 = P1 + ρg y1 − y2( ) = P1 + ρgh . This

is exactly the result we obtained when we looked the forces on a static fluid, namely that the pressure increases

linearly with increasing depth.

Now let’s apply this to a few example problems.

Figure #3: Variation of pressure with depth. D. Giancoli, Physics: Principles with Applications, 7th Ed., Prentice Hall.

Example #1: Fluid exiting a syringe

The body of a syringe is held horizontally and has a cross sectional area Abody = 2.5 ×10−5m2while the needle has a

cross-sectional area of Aneedle = 1.0 ×10−8m2 . Suppose that a force of Fapplied = 2N is applied to the plunger on the

body side of the syringe, what is the speed of the fluid as it leaves the needle’s tip? Assume that the fluid inside

has a density of ρ fluid = 1050kgm3 and that in the absence of the applied force, the pressure on all sides of the syringe

is 1Atm = 1.01×105 Nm2 .

Solution: We apply Bernoulli’s equation to the situation. Defining position 2 to be the needle and position 1 to be

the body of the needle we have: ΔE = 0 = Pneedle − Pbody( ) + 12 ρ fluidvneedle

2 − 12 ρbodyvbody

2( ) . We solve this for the kinetic

energy (per unit volume) of the fluid in the needle and we have 12 ρ fluidvneedle2 = Pbody − Pneedle + 1

2 ρbodyvbody2 . The

pressure applied at the body of the needle is due to atmospheric pressure and the force applied over the cross-

sectional area of the body of the needle. Solving for the speed of the fluid in the needle we have

vneedle2 = 2

Pbody − Pneedleρ fluid

⎛

⎝⎜⎞

⎠⎟+ vbody

2 =2 Fapplied

Abody+ Patm

⎛⎝⎜

⎞⎠⎟ − Patm

⎡⎣⎢

⎤⎦⎥

ρ fluid

+ vbody2 =

2FappliedAbodyρ fluid

+ vbody2 .

To solve for the speed of the fluid exiting the needle, we need to know how fast the fluid is moving in the body of

the needle. Here we will use the equation of continuity, which says that A1v1 = A2v2 → Abodyvbody = Aneedlevneedle .

Therefore solving for the velocity of the fluid in the body of the needle we have vbody =AneedleAbody

⎛

⎝⎜⎞

⎠⎟vneedle . Inserting

this into our equation we can solve for the velocity of the exiting fluid. Substituting we have

vneedle2 =

2FappliedAbodyρ fluid

+ vbody2 =

2FappliedAbodyρ fluid

+ AneedleAbody

⎛

⎝⎜⎞

⎠⎟

2

vneedle2

vneedle2 1− Aneedle

2

Abody2

⎛

⎝⎜⎞

⎠⎟=2FappliedAbodyρ fluid

vneedle =2FappliedAbodyρ fluid

1− Aneedle2

Abody2

⎛

⎝⎜⎞

⎠⎟

−1

= 2 × 2N2.5 ×10−5m2 ×1050 kg

m31−

1.0 ×10−8m2( )22.5 ×10−5m2( )2

⎛

⎝⎜⎜

⎞

⎠⎟⎟

−1

vneedle = 12.3 ms

Comment: Notice Aneedle << Abody that so that when we formed the ratio, the ratio was so small compared to one that

we could have just ignored the term 1− Aneedle2

Abody2

⎛

⎝⎜⎞

⎠⎟

−1

.

Example #2: Lift on an airplane wing

Consider the airplane shown below. What is the aerodynamic lift produced on the wing if the wing has a 60m2

surface area and the velocity of the airflow across the top and bottom of the wing are 340 ms and 290 m

s

respectively? Assume that the wing is thin enough so that the airflow over and under the wing does not have an

appreciable change in height. And in fact, one could argue that the front and back edge of the wing are the same

height, so what ever increase in gravitational potential the air gets going over the front edge it loses when it comes

back down to the back edge, effectively experiencing no net change in height.

Ptop

Pbottom

Figure #4: Photograph of one of the U.S. Air Force Thunderbird aircraft. The red arrows show the pressures on the upper and lower surface of the wings. The difference in pressure gives rise to lift. Photo: S. LaBrake

Solution: We start with Bernoulli’s equation and use the stated assumption.

ΔE = 0 = P2 − P1( ) + 12 ρv2

2 − 12 ρv1

2( ) + ρgy2 − ρgy1( ) = P2 − P1( ) + 12 ρv2

2 − 12 ρv1

2( ) . We notice that since energy is

conserved, where the velocity is higher, by Bernoulli’s equation, the pressure must be lower at that point in order

to keep the energy a fixed quantity. Thus since the velocity of the air is lower on the bottom of the wing, the

pressure must be higher there than on top of the wing and these pressures are shown in figure #4 above. Next we

define position 2 as the bottom of the wing and position 1 the top of the wing. We have (using the density of air as

ρair = 1.3kgm3 )

0 = Pbottom − Ptop( ) + 1

2 ρvbottom2 − 1

2 ρvtop2( )

Pbottom − Ptop = 12 ρairvtop

2 − 12 ρairvbottom

2 = 12 1.3

kgm3( ) 340 m

s( )2 − 290 ms( )2( ) = 20475 N

m2

Now, the pressure is related to the force that’s applied divided by an area. We define the pressure on the bottom

and top of the wings to be FbottomAwing

and FtopAwing

respectively. The difference in forces between the top and bottom of

the wing define the lift Flift = Fbottom − Ftop , which is perpendicular to the wing’s surface. Here since the pressure on

the wing’s bottom is greater than on the wing’s top, the net force is directed vertically upward and the force of lift

acts vertically upward to raise the plane up in the air. Thus we have

Pbottom − Ptop = 20475 Nm2 =

FbottomAwing

−FtopAwing

=FliftAwing

. We can solve for the force of lift and we get

Flift = Awing Pbottom − Ptop( ) = 60m2 × 20475 Nm2 = 1.23×10

6N .

Comment: If the lift force is larger than the weight of the airplane then the airplane accelerates upward at some

rate, call it aplane , and the airplane rises. If the weight of the airplane is greater than the lift (say by the airplane

slowing down its forward velocity) then the plane falls at −aplane . If the weight of the airplane and the lift force are

equal the plane neither rises nor falls but travels forward at a constant velocity. This is provided of course that the

thrust produced by the engines pushing the plane forward equals the drag on the airplane produced by air friction.

Example #3: An old West water tower

Consider a water tower, like one might find in the old West, to be circular with a top that has a cross-sectional area

Atop and the sides a depth d . Further let the water tower be open to air on the top. A Wild West outlaw shoots a

hole in the side of the water tower at a depth h < d below the surface and this hole has a cross-sectional area Aside .

The water flows out of the side of the water tower through the small hole. What is the speed of the water flowing

out of the small hole on the side of the water tower if h = 5m ?

Solution: We apply Bernoulli’s equation and define position 2 to be the hole on the side of the tank and position 1

to be the top of the tank as shown in figure #6 below.

We have ΔE = 0 = Pside − Ptop( ) + 12 ρvside

2 − 12 ρvtop

2( ) + ρgyside − ρgytop( ) . Next we note that the top is open to air and

that the water flowing out of the hole on the side is flowing into air. Thus the pressure on the top and side of the

tank is due to air and Pside = Ptop = Pair . Returning to Bernoulli’s equation we have solving for vside2 :

vside2 = vtop

2 + −2gyside + 2gytop( ) . Defining the zero of the gravitational potential energy to be at ytop , we can solve

for vside . Thus vside = vtop2 − 2g −h( ) = vtop

2 + 2gh . Again, we need to relate the speed of the water moving across

the top surface of the water tower to the speed of the water coming out of the side of the tower. We return to the

equation of continuity and we get A1v1 = A2v2 → Asidevside = Atopvtop → vtop =Aside

Atop⎛⎝⎜

⎞⎠⎟ vside . Assuming that

v2

v1

Figure #6: A tank of water, open to the air on top, with water exiting through a side hole a depth h below the top. This is a model of the “water tower”. D. Giancoli, Physics: Principles with Applications, 7th Ed., Prentice Hall.

Atop >> Aside we have AsideAtop

<<1 and vtop =Aside

Atop⎛⎝⎜

⎞⎠⎟ vside ~ 0 . So, the speed of the water exiting the hole on the side

of the water tower is approximately vside = vtop2 + 2gh ~ 2gh = 2 × 9.8 m

s2 × 5m = 9.9 ms .

Comment: Notice that the density of the fluid disappeared here. This is exactly analogous to dropping a mass m

from rest and letting it fall through a height h . The velocity of the falling mass does not depend on the mass, but

only the height through which it fell.

Example #4: Fluid flow in arteries and veins

Suppose that the aorta has a radius of about raorta = 1.25cm and that the typical blood velocity is around 30 cm

s with an average density of ρ = 1050 kgm3 . A simplified model

of the human circulatory system is shown in Figure #7. The human circulatory system is a closed system, so the flow rate of blood out of the heart has to be the same as the flow rate of blood coming back to the heart. Questions and Solutions:

a. What is the total flow rate of blood through the aorta? r

The total flow rate is determined from the equation of continuity. We have Q = Aaortavaorta = πraorta

2( )vaorta = π 0.0125m( )2 × 0.3 ms = 1.5 ×10

−4 m3s

rr T b. What is the average blood velocity in the major arteries if the total cross-

sectional area of the major arteries is 20cm2 ?

First we convert 20cm2 into square meters. We have 20cm2 × 1m

100cm( )2 = 2 ×10−3m2 . Then we use the equation of continuity to determine the blood velocity in the major arteries. From the equation of

continuity we have Q = Aaortavaorta = Aarteriesvarteries → varteries =Q

Aarteries= 1.5 ×10

−4 m3s

2 ×10−3m2 = 0.075 ms = 7.5 cm

s .

c. On the assumption that all the blood in the circulatory system goes through the capillaries, what is the total cross sectional area of the capillaries if the average velocity of the blood in the capillaries is 0.03 cm

s ?

Again we use the equation of continuity. We have for the total cross-sectional area of all of the capillaries

Q = Aarteriesvarteries = Acapillariesvcapilaies → Acapillaries =Q

vcapilaries= 1.5 ×10

−4 m3s

3×10−4 ms

= 0.5m2 .

Figure #7: Simplified model of the human circulatory system. D. Giancoli, Physics: Principles with Applications, 7th Ed., Prentice Hall.

d. If a typical capillary has a cross sectional area of Acapillary = 3×10−11m2 , about how many capillaries are

there in the human body?

The approximate number of capillaries in the human body is # =AcapillariesAcapillary

= 0.5m2

3×10−11m2 = 1.7 ×1010 or

roughly 17 billion.

e. If a capillary has an average length of l = 0.75mm what is the average time that a red blood cell spends in a capillary?

Assuming that the blood velocity is constant in the capillaries then the average time a red blood cell spends

in a capillary is vcapilary =lt→ t = l

vcapilary= 0.75 ×10

−3m3×10−4 m

s

= 2.5s .

f. What are the kinetic energy per unit volume for blood in the aorta, the major arteries, and the capillaries?

The kinetic energy per unit volume of blood in the major systems is given by KVolume

=12 mv

2

V= 1

2 ρv2 .

Evaluating this for each system we find:

Aorta: KVolume

= 12 ρv

2 = 12 ×1050

kgm2 0.3

ms( )2 = 47.3 J

m3 .

Arteries: KVolume

= 12 ρv

2 = 12 ×1050

kgm2 0.075

ms( )2 = 2.95 J

m3 .

Capillaries: KVolume

= 12 ρv

2 = 12 ×1050

kgm2 3×10

−4 ms( )2 = 4.73×10−5 J

m3 .

Example #5: The Heart as a mechanical pump

The human heart can be modeled as a mechanical pump. The aorta is a large artery that carries oxygenated blood

away from the heart to various organs in the body. For an individual at rest, the blood (

�

ρblood =1050 kgm 3 ) in the aorta

of radius

�

raorta =1.25cm flows at a rate of

�

5 ×10−4 m 3

min . In what follows, we will be talking about power. Power is

the rate at which work is done or the rate at which energy is transferred into or out of a system by an external force.

Thus we can define the work done on an object as P = ΔEΔt

= ΔWΔt

= FΔxΔt

= Fv in units of Joules per second or

equivalently Watts, where 1W = 1 Js .

Questions and Solutions:

a. With every beat, the heart does work moving the blood into the aorta. The heart does work at a rate of

�

0.5 Js . Derive an expression for the energy per unit volume of blood associated with the blood flow into the

aorta?

We start with the expression for power and we see that the question ask us to determine an expression for

the energy per unit volume. Thus we will take our equation for power and multiply it by a factor of one.

This will generate the energy per unit volume we seek. In addition we generate an extra term that, the

volume of blood flow per unit time. This is simply the flow rate, which we will call Q . Thus we have

P = ΔEΔt

× VolumeVolume

= ΔEVolume

× VolumeΔt

= ΔEVolume

×Q and the energy per unit volume is ΔEVolume

= PQ

.

Using the numbers given in the problem we can calculate a value for this quantity, namely

ΔEVolume

= PQ

= 0.5 Js

5×10−4m360s

= 60000 Jm3 = 60000

Nm2 .

b. The energy per unit volume (or kinetic energy per unit volume) of a moving fluid corresponds to a

difference in pressure between two different points in space. Suppose you have the condition called

atherosclerosis. Atherosclerosis is a disease in which plaque builds up inside walls of your arteries.

Arteries are blood vessels that carry oxygen-rich blood to your heart and other parts of your body. Plaque is

made up of fat, cholesterol, calcium, and other substances found in the blood. Over time, plaque hardens

and narrows your arteries and constricts blood flow. This limits the flow of oxygen-rich blood to your

organs and other parts of your body. Atherosclerosis can lead to serious problems, including heart attack,

stroke, or even death.). Suppose that you had the condition of atherosclerosis, what would be the radius of

the opening that remains and what percent of the aorta would be blocked? Assume that the buildup on the

walls of the aorta is uniform so that the opening that remains is circular and that the patient is lying

horizontal. The situation is shown in Figure #8 below.

In order to answer the question of how much of the aorta is blocked, we first calculate the speed of the

blood in the unblocked portion of the aorta. We can calculate this speed from the flow rate and the cross-

sectional area of the aorta. From the information given in the problem, we have the flow rate where

Q = Aaortavaorta and thus vaorta =QAaorta

=5.4×10−4m3

60s

π 0.0125m( )2= 0.017 m

s .Next we turn to Bernoulli’s equation and

for a person who is lying horizontally, the difference in pressure between the unblocked and blocked

portion of the aorta is P1 + 12 ρv1

2 + ρgy1 = P2 + 12 ρv2

2 + ρgy2 . Defining position 1 to be in the unblocked

aorta and position 2 in the blockage, we have Paorta + 12 ρvaorta

2 = Pblockage + 12 ρvblockage

2 . Solving for the speed of

the blood flow in the blockage we get

vblockage =2ρPaorta − Pblockage( ) + vaorta2 =

2 60000 Nm2( )

1050 kgm3

+ 0.017 ms( )2 = 10.1 m

s . Having now calculated the

speed of the blood in the blockage and since the flow rate is continuous, we can determine the area of the

blockage. From the area we can determine the radius of the blockage and what percent is blocked. The

area of the blockage can be determined from the flow rate. The flow rate and area of the blockage are

Q = Ablockagevblockage → Ablockage =Q

vblockage=

5.4×10−4m360s

10.7 ms

= 8.41×10−7m2 . Therefore the radius of the blockage,

assuming that the blockage is circular is given by

Ablockage = πrblockage2 → rblockage =

Ablockageπ

= 8.41×10−7m2

π= 0.0005m = 0.05cm .

Blockage

Blockage

FromHearttoBody

Figure #8 Cartoon model of the human aorta with a blockage for a person lying horizontally.

Lastly the percent of the aorta that is blocked is

�

% =ri − rfri

⎡

⎣ ⎢

⎤

⎦ ⎥ ×100% = 1.25cm − 0.05cm

1.25cm⎡ ⎣ ⎢

⎤ ⎦ ⎥ ×100% = 96%.