Entangling two distinguishable quantum bright solitons via collisions

Entangling two distinguishable quantum bright solitons via collisions

Thomas P. BillamJack Dodd Center for Quantum Technology, Department of Physics,

University of Otago, Dunedin 9016, New Zealand

Caroline L. BlackleyJoint Quantum Centre (JQC) Durham–Newcastle, Department of Chemistry,

Durham University, Durham DH1 3LE, United Kingdom

Bettina GertjerenkenInstitut fur Physik, Carl von Ossietzky Universitat, D-26111 Oldenburg, Germany

Simon L. Cornish and Christoph Weiss∗

Joint Quantum Centre (JQC) Durham–Newcastle, Department of Physics,Durham University, Durham DH1 3LE, United Kingdom

(Dated: January 6, 2014)

The generation of mesoscopic Bell states via collisions of distinguishable bright solitons has beensuggested in Phys. Rev. Lett. 111, 100406 (2013). Here, we extend our former proposal to two hy-perfine states of 85Rb instead of two different atomic species, thus simplifying possible experimentalrealisations. A calculation of the s-wave scattering lengths for the hyperfine states (f,mf ) = (2,+2)and (3,+2) identifies parameter regimes suitable for the creation of Bell states with an advanta-geously broad Feshbach resonance. We show the generation of Bell states using the truncatedWigner method for the soliton’s centre of mass and demonstrate the validity of this approach by acomparison to a mathematically rigorous effective potential treatment of the quantum many-particleproblem.

I. INTRODUCTION

Bright solitons are a promising candidate to gener-ate quantum entanglement for a mesoscopic number ofatoms. Such bright solitons are realised experimentallyin Bose-Einstein condensates [1–6]. These experimentshave thus far been modelled by a mean-field descrip-tion. However, going to lower particle numbers naturallyrequires a fuller quantum mechanical treatment. Thequantum bright solitons described by such a treatmentprovide an excellent model system with which to investi-gate the “middle-ground” between quantum and classicalphysics [7, 8].

Scattering bright solitons off a single barrier was re-cently investigated in [9–18] and references therein; withtwo barriers a soliton diode was suggested in [19]. In theregime of very low kinetic energies [20–22], scattering aquantum bright soliton [23–28] off a barrier can even leadto Schrodinger cat states [20, 21] that can be detected us-ing their interference properties [18, 20].

Schrodinger-cat states are highly non-classicalsuperpositions[29] which are relevant for quantum-enhanced interferometry [30]. The focus of our paperare mesoscopic Bell states

|ψBell〉 ≡1√2

(|A,B〉+ eiα|B,A〉

), (1)

∗ [email protected]

where |A,B〉 (|B,A〉) signifies that the BEC A is on theleft (right) and the BEC B is on the right (left). While itmight sound tempting to realise such mesoscopic quan-tum superpositions as, say, the ground states of Bose-Einstein condensate in a double well with carefully cho-sen signs and strengths of interactions, such an approachwill not be successful in the presence of tiny asymme-tries (cf. [31]) and decoherence. Suggestions of how sucha state can be realised dynamically for Bose-Einstein con-densates can be found in Refs. [31–36] and referencestherein.

Rather than using a potential to generate mesoscopicentanglement [20, 21], we have suggested to scatter twodistinguishable quantum bright solitons off each otherto generate mesoscopic Bell states [37]. Two collidingdistinguishable bright solitons behave very differentlyfrom two colliding but initially indistinguishable soli-tons [38, 39]: for indistinguishable solitons, either higherorder nonlinear terms [38] (cf. [40]) or additional har-monic confinement [39] are needed to generate entangle-ment. Quantum bright solitons have also been discussedin the context of symmetry breaking states [26]; for moregeneral treatment of symmetry breaking in finite quan-tum systems see [41] and references therein.

In this paper we discuss the generation of a mesoscopicBell state via scattering two distinguishable bright soli-tons. While our original proposal [37] scattered two soli-tons of different species (85Rb and 133Cs), we now sug-gest to use two hyperfine states of 85Rb. This allows thegeneration of mesoscopic Bell states closer to the case ofmany photons which is an area of current theoretical and

arX

iv:1

401.

0666

v1 [

cond

-mat

.qua

nt-g

as]

3 J

an 2

014

2

experimental research [42, 43]. In addition to their in-herent fundamental interest, such states are of potentialapplication as a resource in quantum information [43].

Our paper is organised as follows: We first introducethe many-particle quantum model used to describe thetwo colliding solitons in sec. II before justifying our useof a classical field approach to describe mesoscopic quan-tum superpositions in sec. III. In sec. IV we describe anew Feshbach resonance, offering excellent control overdistinguishable soliton collisions, which we use for ournumerics in sec. V. In sec. VI we present signatures thatdistinguish quantum superpositions from statistical mix-tures. The paper ends with the conclusions in sec. VII.

II. MODEL

In order to model two distinguishable solitons on themany-particle quantum level, we use the same approachas [37] and set mA = mB at the end, where mA (mB) isthe atomic mass of species A (B) (as we have two hyper-fine states of the same species). For our quasi-1D system,we consider an experimentally motivated harmonic con-finement ω = 2πf . Mixtures of ultracold gases can beconfined in a common optical trap with the same trapfrequencies [44], yielding

ω =2π

T; λA =

√~

mAω; λB =

√~

mBω, (2)

where λA and λB are the harmonic oscillator lengths ofthe two species; the interactions gS = hf⊥aS are setby the scattering lengths aS (S = A,B or AB) and theperpendicular trapping-frequency, f⊥ [45].

We use the Lieb-Liniger model [46, 47] for two specieswith additional harmonic confinement

H =−NA∑j=1

~2

2mA∂2xj

+

NA−1∑j=1

NA∑n=j+1

gAδ (xj − xn)

−NB∑j=1

~2

2mB∂2yj +

NB−1∑j=1

NB∑n=j+1

gBδ (yj − yn)

+

NA∑j=1

NB∑n=1

gABδ (xj − yn)

+

NA∑j=1

1

2mAω

2x2j +

NB∑j=1

1

2mBω

2y2j , (3)

where xj (yj) and gA < 0 (gB < 0) are the atomic co-ordinates and intra-species interactions of species A (B),and gAB ≥ 0 is the inter-species interaction.

We suggest to prepare the two solitons independently;for weak harmonic confinement a single soliton has theground state energy (cf. [48])

ES(NS) = − 1

24

mSg2S

~2NS(N2

S − 1) ; S ∈ {A,B} . (4)

Thus, our system has the total ground-state energy

E0 = EA(NA) + EB(NB) . (5)

The total kinetic energy related to the centre-of-mass mo-menta ~KS ( S ∈ {A,B}) of the two solitons reads

Ekin =~2K2

A

2NAmA+

~2K2B

2NBmB. (6)

We extend the low-energy regime investigated forsingle-species solitons in Refs. [20, 22, 49] to two species:

Ekin < min{∆A,∆B}, ∆S = |ES(NS − 1)− ES(NS)| .

In this energy regime, each of the quantum matter-wavebright solitons is energetically forbidden to break up intotwo or more parts. Highly entangled states are charac-terised by a roughly 50:50 chance of finding the soliton A(B) on the left/right combined with a left/right correla-tion close to one indicating that whenever soliton A is onthe one side, soliton B is on the other:

γ(δ) ≡∫ ∞δ

dx1 . . .

∫ ∞δ

dxNA

∫ −δ−∞

dy1 . . .

∫ −δ−∞

dyNB|Ψ|2

+

∫ −δ−∞

dx1 . . .

∫ −δ−∞

dxNA

∫ ∞δ

dy1 . . .

∫ ∞δ

dyNB|Ψ|2 ,

(7)

where Ψ = Ψ(x1, . . . , xNA, y1, . . . , yNB

) is the many-particle wave function (normalised to one) and δ ≥ 0.The correlation γ(δ) will serve as an indication of en-tanglement: Bell states (1) are characterised by γ ' 1combined with a 50:50 chance to find soliton A either onone side or on the other.

Behaviour for larger particle numbers can be describedby the Gross-Pitaevskii equation (GPE) (cf. [50–53])

i~∂tϕA(x, t) =

[− ~2

2mA∂2x +

gA2|ϕA(x, t)|2

]ϕA(x, t)

+

[1

2mAω

2x2 +gAB

2|ϕB(x, t)|2

]ϕA(x, t)

i~∂tϕB(x, t) =

[− ~2

2mB∂2x +

gB2|ϕB(x, t)|2

]ϕB(x, t)

+

[1

2mBω

2x2 +gAB

2|ϕA(x, t)|2

]ϕB(x, t) ,

where the single-particle density |ϕS(x, t)|2 is normalisedto NS (S ∈ {A,B}).

III. JUSTIFYING TRUNCATED WIGNER FORTHE CENTRE OF MASS

When hitting a barrier, the generic behaviour of amean-field bright soliton is to break into two parts; thefraction of the atoms transmitted decreases for increasing

3

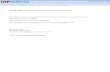
FIG. 1. (a) Single-particle density for a N -particle quantum bright soliton (soliton A) hitting a narrow, heavy non-movingsoliton (soliton B), computed using the effective potential approach, as in ref. [37]. (b) GPE simulation, using centre-of-massTW technique, of a single N -particle quantum bright soliton colliding with the same single-particle potential due to soliton B asin the effective potential treatment. Taking mA = mB = m and NBgB = 10NAgA, the system can be described in terms of theharmonic oscillator length λ ≡ λA; we choose parameters such that the mean initial displacement of the soliton −0.48λ and thesingle-particle potential V (x) = A~ωsech2(3x/2λ) with A ≈ 1.2 [37]. NA = 100. TW results averaged over 1000 realisations.

potential strength (cf. [12, 14]). An analogous behaviouralso occurs when two distinguishable mean-field brightsolitons collide with each other, as shown in the Supple-mental Material of [37]. Only at very low kinetic ener-gies [20, 22, 37] do mesoscopic quantum superpositionsoccur as a result of such collisions.

To describe low kinetic energy collisions of two dis-tinguishable bright solitons, taking into account the for-mation of mesoscopic quantum superpositions, we com-bine mean-field calculations via the GPE with Truncated-Wigner Approximation (TWA) for the centre of massdegree of freedom in order to model true quantumbehaviour [37]. The truncated-Wigner approximation(TWA) describes quantum systems by averaging over re-alisations of an appropriate classical field equation (inthis case, the GPE) with initial noise appropriate to ei-ther finite [54] or zero temperatures [12]. While the GPEassumes both position and momentum are well-defined,this is not true for a single quantum particle of finitemass for which, in general, both position and momen-tum involve quantum noise satisfying the uncertainty re-lation. Our TWA calculations for the soliton centre-of-mass wave function use Gaussian probability distribu-tions for both (satisfying minimal uncertainty) [37].

This centre-of-mass TW technique can be justified bycomparison to the rigorously proved [55] effective poten-tial approach [20, 49]: In fig. 1 we compare the single-particle effective potential treatment [fig. 1(a)] for thecase of a low-mass bright soliton colliding with a heavybright soliton with a centre-of-mass TW GPE simulation[fig. 1(b)] using the same effective single-particle poten-tial. In the low kinetic energy regime considered, thelow-mass bright soliton is either completely reflected orcompletely transmitted in any individual realisation. Thegood level of agreement up to the time where the soli-tons re-collide confirms that the centre-of-mass TW tech-nique can successfully capture the dynamical formationof quantum superpositions in the centre-of-mass coordi-

nate, as required.

IV. SUITABLE FESHBACH RESONANCE

Using mixed states of the same atomic species allowsfor the creation of distinguishable solitons while removingthe need for a dual-species laser cooling apparatus. Thephysical requirements for the experiment are a negativebackground scattering length for each of the two distin-guishable soliton states, and a wide Feshbach resonancein the mixed-state scattering length.

Coupled-channels calculations were performed as de-tailed in Ref [56] on each of the (fa, fb) = (2, 3) hyper-fine manifold of 85Rb2, using the molscat program [57]adapted to handle collisions in external fields [58]. A widetunable resonance was found in the (fa,mfa)(fb,mfb) =(2, 2)(3, 2) channel. The resonance has a width of∆=14 G determined by the difference between the zero-crossing and the pole in the scattering length. Whilstexcited-state resonances are subject to decay from in-elastic collisions [59] the resonance has ares > 10, 000 a0making it ‘pole-like’ from an experimental point of view.In the excited states the complex scattering length isgiven by a(B) = α(B) − iβ(B), where α(B) is the realpart of the scattering length, and β(B) the imaginarypart of the scattering length is proportional to the rate-coefficient for 2-body losses due to inelastic collisions,Kloss = 2h

µ gnβ(B), where gn=1 (2) for a BEC of dis-

tinguishable (indistinguishable) particles. The real partof the scattering length and associated plots of Kloss, ofboth the mixed-state and the individual states, are shownin fig. 2. Note that Kloss = 0 for the absolute internalground state (f,mf ) = (2,+2).

The three-dimensional scattering calculations can beconverted into a one dimensional interaction parameterg by taking account of the trapping frequency (f⊥). With

4

FIG. 2. The s-wave scattering lengths for the (f,mf)= (2,+2),(3,+2) and (2,+2)+(3,+2) states of 85Rb. (a) The scatteringlength is split into real and imaginary components, the realpart is shown in the top plot, the imaginary part is propor-tional to the inelastic decay rate-coefficent Kloss, shown inthe lower graph. (b) Zoom of (a), the wide resonance in themixed spin state allows for tuning of the scattering length.

the introduction of the trapping parameters it is possi-ble to cause a confinement induced resonance (CIR) aspredicted in [60] when a⊥ ≈ Ca3D. However, given theconfinement parameters for this problem (f⊥ = 50 Hzand f = 2 Hz, see fig. 3), the CIR would occur whena3D ≈ 3.5 × 105a0 which would not interfere with anypractical implementation.

V. TRUNCATED WIGNER FOR THE CENTREOF MASS FOR TWO DISTINGUISHABLE

BRIGHT SOLITONS

Using the Feshbach resonance described in the previ-ous section we perform a centre-of-mass TW GPE simu-lation for the two-component GPE using parameters for

a mixture of the (f,mf ) = (2,+2) and (3,+2) hyperfinestates of 85Rb. The resulting average density profiles forthe two components, and the left/right correlation γ(0)are shown in fig. 3. The high (≈ 1) value of γ(0) sub-sequent to the first collision indicates the formation ofa Bell state with high fidelity. Compared to the 85Rb –133Cs scheme suggested in ref. [37], the present schemeis feasible at higher atom numbers, less sensitive to mag-netic bias field strength, and generates higher-fidelity Bellstates. These factors make the present scheme an evenmore experimentally attractive proposal to generate Bellstates of distinguishable bright solitons.

VI. DISTINGUISHING QUANTUMSUPERPOSITIONS FROM STATISTICAL

MIXTURES

Bell inequalities, which are both interesting becausethey allow to fundamentally test our understanding ofquantum mechanics [61, 62] and because of their impor-tance for quantum cryptography [63], are still a topic ofcurrent research [64]. For mesoscopic Bell states, relatedseparability conditions are available [43, 65]. For a bi-partite photonic system a violation of the inequality

3∑k=1

∆S2k/〈S0〉 ≥ 2 (8)

has been shown to be a sufficient condition of non-separability and has been used to identify polarisationentanglement for squeezed vacuum pulses [43]. Here,Sk = SAk + SBk denote the Stokes parameters [65] and〈S0〉 is the total photon number. To convey condition (8)to our situation the properties left and right would takeon the role of horizontal and vertical polarisation.

In addition to the above, in the collisions we considerhere the interference properties discussed in [37] for twodifferent species would also be available to distinguishquantum superpositions from statistical mixtures.

VII. CONCLUSION

We have investigated numerically the generation ofmesoscopic Bell states via the collision of two distinguish-able quantum bright solitons. For experimentally realis-tic parameters, we have used Truncated Wigner for thecentre of mass [37] (which we justified further) to predictentanglement generation. We have in particular extendedthe scheme suggested in [37] for two bright solitons of twodifferent species to two solitons of two distinct hyperfinestates of the same species, providing several advantagescompared to the original suggestion [37]:

1. We predict a much broader Feshbach resonance(fig. 2 b) then for the two-species case investigatedin [37]. This will considerably simplify future ex-periments.

5

FIG. 3. Centre-of-mass TW GPE simulation of a two-component collision of solitons in the (f,mf ) = (2,+2) and (3,+2)hyperfine states of 85Rb. Parameters are a(2,2) = −410a0, a(3,2) = −460a0, N(2,2) = N(3,2) ≈ 90, f = 2 Hz, f⊥ = 50 Hz, anda(2,2)/(3,2) ' 30.0a0 (conveniently reached at around 295 G, see fig. 2). The initial displacement of the solitons is ≈ ±10.1µm.Panels (a), (b) and (c) respectively show the average single-particle densities of the (2, 2) and (3, 2) components, and theleft/right correlation γ(0). 1000 realisations were performed.

2. We predict a higher left/right correlation in the Bellstate (fig. 3 c), potentially aiding experimental de-tection.

3. Only a Bose-Einstein condensate of one speciesis required; the two distinguishable bright soli-tons could be produced from a single initial Bose-Einstein condensate.

4. The current situation is closer to the mesoscopicBell states for photons of refs. [42, 43].

ACKNOWLEDGMENTS

We thank S. A. Gardiner, J. L. Helm, J. M. Hutson, C.R. Le Sueur, L. Khaykovich for discussions. We thank the

Marsden Fund of New Zealand (Contract No. UOO162)and the Royal Society of New Zealand (Contract No.UOO004) (T. P. B.), the Faculty of Science at DurhamUniversity (C. L. B.), and the UK EPSRC (Grant No.EP/G056781/1 and EP/K03250X/1) (C. W.) for fund-ing.

REFERENCES

[1] L. Khaykovich, F. Schreck, G. Ferrari, T. Bourdel, J. Cu-bizolles, L. D. Carr, Y. Castin, and C. Salomon, Science296, 1290 (2002)

[2] K. E. Strecker, G. B. Partridge, A. G. Truscott, and R. G.Hulet, Nature (London) 417, 150 (2002)

[3] B. Eiermann, T. Anker, M. Albiez, M. Taglieber,P. Treutlein, K.-P. Marzlin, and M. K. Oberthaler, Phys.Rev. Lett. 92, 230401 (Jun 2004)

[4] S. L. Cornish, S. T. Thompson, and C. E. Wieman, Phys.Rev. Lett. 96, 170401 (2006)

[5] S. E. Pollack, D. Dries, E. J. Olson, andR. G. Hulet, 2010 DAMOP: Conference abstract,http://meetings.aps.org/link/BAPS.2010.DAMOP.R4.1

[6] A. L. Marchant, T. P. Billam, T. P. Wiles, M. M. H. Yu,S. A. Gardiner, and S. L. Cornish, Nat. Commun. 4, 1865(2013)

[7] L. Hackermuller, K. Hornberger, B. Brezger, A. Zeilinger,and M. Arndt, Nature (London) 427, 711 (2004)

[8] W. H. Zurek, Rev. Mod. Phys. 75, 715 (2003)[9] T. Ernst and J. Brand, Phys. Rev. A 81, 033614 (2010)

6

[10] C.-H. Wang, T.-M. Hong, R.-K. Lee, and D.-W. Wang,Opt. Express 20, 22675 (2012)

[11] S. Damgaard Hansen, N. Nygaard, and K. Mølmer,Preprint arXiv:1210.1681(2012)

[12] A. D. Martin and J. Ruostekoski, New J. Phys. 14,043040 (2012)

[13] J. L. Helm, T. P. Billam, and S. A. Gardiner, Phys. Rev.A 85, 053621 (2012)

[14] J. Cuevas, P. G. Kevrekidis, B. A. Malomed, P. Dyke,and R. G. Hulet, New J. Phys. 15, 063006 (2013)

[15] A. Alvarez, J. Cuevas, F. R. Romero, C. Hamner,J. J. Chang, P. Engels, P. G. Kevrekidis, and D. J.Frantzeskakis, J. Phys. B 46, 065302 (2013)

[16] J. Polo and V. Ahufinger, Phys. Rev. A 88, 053628 (2013)[17] T. Fogarty, A. Kiely, S. Campbell, and T. Busch, Phys.

Rev. A 87, 043630 (2013)[18] B. Gertjerenken, Phys. Rev. A 88, 053623 (2013)[19] M. Asad-uz-zaman and U. A. Khawaja, EPL (Europhys.

Lett.) 101, 50008 (2013)[20] C. Weiss and Y. Castin, Phys. Rev. Lett. 102, 010403

(2009)[21] A. I. Streltsov, O. E. Alon, and L. S. Cederbaum, Phys.

Rev. A 80, 043616 (2009)[22] B. Gertjerenken, T. P. Billam, L. Khaykovich, and

C. Weiss, Phys. Rev. A 86, 033608 (2012)[23] S. J. Carter, P. D. Drummond, M. D. Reid, and R. M.

Shelby, Phys. Rev. Lett. 58, 1841 (1987)[24] Y. Lai and H. A. Haus, Phys. Rev. A 40, 854 (1989)[25] P. D. Drummond, R. M. Shelby, S. R. Friberg, and Y. Ya-

mamoto, Nature (London) 365, 307 (1993)[26] Y. Castin and C. Herzog, C. R. Acad. Sci. Paris, Ser. IV

2, 419 (2001), arXiv:cond-mat/0012040[27] L. D. Carr and J. Brand, Phys. Rev. Lett. 92, 040401

(2004)[28] D. Delande, K. Sacha, M. P lodzien, S. K. Avazbaev, and

J. Zakrzewski, New J. Phys. 15, 045021 (2013)[29] In a measurement, all particles would be on one side of

the barrier; before the measurement, they were in a quan-tum superposition of all being on the right and all beingon the left.

[30] V. Giovannetti, S. Lloyd, and L. Maccone, Science 306,1330 (2004)

[31] C. Weiss and N. Teichmann, Laser Phys. Lett. 4, 895(2007)

[32] A. Micheli, D. Jaksch, J. I. Cirac, and P. Zoller, Phys.Rev. A 67, 013607 (2003)

[33] K. W. Mahmud, H. Perry, and W. P. Reinhardt, Phys.Rev. A 71, 023615 (2005)

[34] D. Dagnino, N. Barberan, M. Lewenstein, and J. Dal-ibard, Nature Phys. 5, 431 (2009)

[35] M. A. Garcia-March, D. R. Dounas-Frazer, and L. D.Carr, Phys. Rev. A 83, 043612 (2011)

[36] G. Mazzarella, L. Salasnich, A. Parola, and F. Toigo,Phys. Rev. A 83, 053607 (2011)

[37] B. Gertjerenken, T. P. Billam, C. L. Blackley, C. R.Le Sueur, L. Khaykovich, S. L. Cornish, and C. Weiss,

Phys. Rev. Lett. 111, 100406 (2013)[38] M. Lewenstein and B. A. Malomed, New J. Phys. 11,

113014 (2009)[39] D. I. H. Holdaway, C. Weiss, and S. A. Gardiner, Phys.

Rev. A 87, 043632 (2013)[40] L. Khaykovich and B. A. Malomed, Phys. Rev. A 74,

023607 (2006)[41] J. Birman, R. Nazmitdinov, and V. Yukalov, Phys. Rep.

526, 1 (2013)[42] M. Stobinska, F. Toppel, P. Sekatski, and M. V.

Chekhova, Phys. Rev. A 86, 022323 (2012)[43] T. S. Iskhakov, I. N. Agafonov, M. V. Chekhova, and

G. Leuchs, Phys. Rev. Lett. 109, 150502 (2012)[44] M. S. Safronova, B. Arora, and C. W. Clark, Phys. Rev.

A 73, 022505 (2006)[45] T. Bergeman, M. G. Moore, and M. Olshanii, Phys. Rev.

Lett. 91, 163201 (2003)[46] E. H. Lieb and W. Liniger, Phys. Rev. 130, 1605 (1963)[47] R. Seiringer and J. Yin, Commun. Math. Phys. 284, 459

(2008)[48] J. B. McGuire, J. Math. Phys. 5, 622 (1964)[49] K. Sacha, C. A. Muller, D. Delande, and J. Zakrzewski,

Phys. Rev. Lett. 103, 210402 (2009)[50] H. Pu and N. P. Bigelow, Phys. Rev. Lett. 80, 1134

(1998)[51] E. Timmermans, Phys. Rev. Lett. 81, 5718 (1998)

[52] P. Ohberg and L. Santos, Phys. Rev. Lett. 86, 2918(2001)

[53] He, Z.M., Wang, D.L., Ding, J.W., and Yan, X.H., Eur.Phys. J. D 66, 139 (2012)

[54] P. Bienias, K. Pawlowski, M. Gajda, and K. Rzazewski,EPL (Europhys. Lett.) 96, 10011 (2011)

[55] C. Weiss and Y. Castin, J. Phys. A 45, 455306 (2012)[56] C. L. Blackley, C. R. Le Sueur, J. M. Hutson, D. J. Mc-

Carron, M. P. Koppinger, H.-W. Cho, D. L. Jenkin, andS. L. Cornish, Phys. Rev. A 87, 033611 (2013)

[57] J. M. Hutson and S. Green, “MOLSCAT computer pro-gram, version 14,” distributed by Collaborative Compu-tational Project No. 6 of the UK Engineering and Phys-ical Sciences Research Council (1994)

[58] M. L. Gonzalez-Martınez and J. M. Hutson, Phys. Rev.A 75, 022702 (2007)

[59] J. M. Hutson, New J. Phys. 9, 152 (2007)[60] M. Olshanii, Phys. Rev. Lett. 81, 938 (1998)[61] J. F. Clauser and A. Shimony, Reports on Progress in

Physics 41, 1881 (1978)[62] A. Aspect, J. Dalibard, and G. Roger, Phys. Rev. Lett.

49, 1804 (1982)[63] A. K. Ekert, Phys. Rev. Lett. 67, 661 (1991)[64] G. Torlai, G. McKeown, P. Marek, R. Filip, H. Jeong,

M. Paternostro, and G. De Chiara, Phys. Rev. A 87,052112 (2013)

[65] C. Simon and D. Bouwmeester, Phys. Rev. Lett. 91,053601 (2003)