Bayesian Poisson Tucker Decomposition for Learning the ...aschein/ScheinZhouBleiWallach2016_paper.pdf1 c=1 P 1 d=1 P 1 k=1 P 1 r=1 (r) c! kd 1 c, d, , r from a gamma process, provided

Bayesian Poisson Tucker Decompositionfor Learning the Structure of International Relations

Aaron Schein [email protected]

University of Massachusetts Amherst

Mingyuan Zhou [email protected]

University of Texas at Austin

David M. Blei [email protected]

Columbia University

Hanna Wallach [email protected]

Microsoft Research New York City

AbstractWe introduce Bayesian Poisson Tucker de-composition (BPTD) for modeling country–country interaction event data. These data con-sist of interaction events of the form “coun-try i took action a toward country j at timet.” BPTD discovers overlapping country–community memberships, including the numberof latent communities. In addition, it discoversdirected community–community interaction net-works that are specific to “topics” of action typesand temporal “regimes.” We show that BPTDyields an efficient MCMC inference algorithmand achieves better predictive performance thanrelated models. We also demonstrate that it dis-covers interpretable latent structure that agreeswith our knowledge of international relations.

1. IntroductionLike their inhabitants, countries interact with one another:they consult, negotiate, trade, threaten, and fight. Theseinteractions are seldom uncoordinated. Rather, they areconnected by a fabric of overlapping communities, such assecurity coalitions, treaties, trade cartels, and military al-liances. For example, OPEC coordinates the petroleum ex-port policies of its thirteen member countries, LAIA fosterstrade among Latin American countries, and NATO guaran-tees collective defense against attacks by external parties.

Proceedings of the 33 rd International Conference on MachineLearning, New York, NY, USA, 2016. JMLR: W&CP volume48. Copyright 2016 by the author(s).

A single country can belong to multiple communities, re-flecting its different identities. For example, Venezuela—an oil-producing country and a Latin American country—isa member of both OPEC and LAIA. When Venezuela inter-acts with other countries, it sometimes does so as an OPECmember and sometimes does so as a LAIA member.

Countries engage in both within-community and between-community interactions. For example, when acting asan OPEC member, Venezuela consults with other OPECcountries, but trades with non-OPEC, oil-importing coun-tries. Moreover, although Venezuela engages in between-community interactions when trading as an OPEC member,it engages in within-community interactions when tradingas a LAIA member. To understand or predict how countriesinteract, we must account for their community member-ships and how those memberships influence their actions.

In this paper, we take a new approach to learning over-lapping communities from interaction events of the form“country i took action a toward country j at time t.” A dataset of such interaction events can be represented as either1) a set of event tokens, 2) a tensor of event type counts, or3) a series of weighted multinetworks. Models that use thetoken representation naturally yield efficient inference al-gorithms, models that use the tensor representation exhibitgood predictive performance, and models that use the net-work representation learn latent structure that aligns withwell-known concepts such as communities. Previous mod-els of interaction event data have each used a subset of theserepresentations. Our approach—Bayesian Poisson Tuckerdecomposition (BPTD)—takes advantage of all three.

Bayesian Poisson Tucker Decomposition for Learning the Structure of International Relations

1 2 3 4 5 6 7 8 9 10 11 12Estonia

DenmarkSloveniaFinlandSweden

Holy SeeAustria

LithuaniaSwitzerland

LatviaHungary

NetherlandsBelgiumBulgariaSlovakiaRomania

Czech Rep.PolandCroatia

ItalyGermany

FranceMacedonia

CyprusGreeceTurkey

MontenegroKosovoAlbaniaBosniaSerbia

1 2 3 4 5 6 7 8 9 10 11 12

1211

109

87

65

43

21

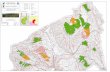
Figure 1. Latent structure learned by BPTD from country–country interaction events between 1995 and 2000. Top right:A community–community interaction network specific to a singletopic of action types and temporal regime. The topic places mostof its mass on the Intend to Cooperate and Consult actions, sothis network represents cooperative community–community in-teractions. The two strongest between-community interactions(circled) are 2�!5 and 2�!7. Left: Each row depicts the over-lapping community memberships for a single country. We showonly those countries whose strongest community membership isto either community 2, 5, or 7. We ordered the countries ac-cordingly. Countries strongly associated with community 7 areat highlighted in red; countries associated with community 5 arehighlighted in green; and countries associated with community2 are highlighted in purple. Bottom right: Each country is col-ored according to its strongest community membership. The la-tent communities have a very strong geographic interpretation.

BPTD builds on the classic Tucker decomposition (Tucker,1964) to factorize a tensor of event type counts into threefactor matrices and a four-dimensional core tensor (sec-tion 2). The factor matrices embed countries into com-munities, action types into “topics,” and time steps into“regimes.” The core tensor interacts communities, top-ics, and regimes. The country–community factors en-able BPTD to learn overlapping community member-ships, while the core tensor enables it to learn directedcommunity–community interaction networks specific totopics of action types and temporal regimes. Figure 1 il-lustrates this structure. BPTD leads to an efficient MCMCinference algorithm (section 4) and achieves better predic-tive performance than related models (section 6). Finally,BPTD discovers interpretable latent structure that agreeswith our knowledge of international relations (section 7).

2. Bayesian Poisson Tucker DecompositionWe can represent a data set of interaction events as a setof N event tokens, where a single token en = (i

a�!j, t)indicates that sender country i 2 [V ] took action a 2 [A]toward receiver country j 2 [V ] during time step t 2 [T ].Alternatively, we can aggregate these event tokens into afour-dimensional tensor Y , where element y(t)

ia�!j

is a count

of the number of events of type (ia�!j, t). This tensor will

be sparse because most event types never actually occurin practice. Finally, we can equivalently view this counttensor as a series of T weighted multinetwork snapshots,where the weight on edge i

a�!j in the tth snapshot is y(t)i

a�!j.

BPTD models each element of count tensor Y as

y(t)

ia�!j

⇠ Po

CX

c=1

✓ic

CX

d=1

✓jd

KX

k=1

�ak

RX

r=1

tr �(r)

ck�!d

!, (1)

where ✓ic, ✓jd, �ak, tr, and �(r)c

k�!dare positive real num-

bers. Factors ✓ic and ✓jd capture the rates at which coun-tries i and j participate in communities c and d, respec-tively; factor �ak captures the strength of association be-tween action a and topic k; and tr captures how wellregime r explains the events in time step t. We can col-lectively view the V ⇥ C country–community factors as alatent factor matrix⇥, where the ith row represents countryi’s community memberships. Similarly, we can view theA⇥K action–topic factors and the T⇥R time-step–regimefactors as latent factor matrices � and , respectively. Fac-tor �(r)

ck�!d

captures the rate at which community c takes ac-tions associated with topic k toward community d duringregime r. The C ⇥ C ⇥ K ⇥ R such factors form a coretensor ⇤ that interacts communities, topics, and regimes.

The country–community factors are gamma-distributed,

✓ic ⇠ �(↵i,�i) , (2)

where the shape and rate parameters ↵i and �i are specificto country i. We place an uninformative gamma prior overthese shape and rate parameters: ↵i,�i ⇠ �(✏0, ✏0). Thishierarchical prior enables BPTD to express heterogeneityin the countries’ rates of activity. For example, we expectthat the US will engage in more interactions than Burundi.

The action–topic and time-step–regime factors are alsogamma-distributed; however, we assume that these factorsare drawn directly from an uninformative gamma prior,

�ak, tr ⇠ �(✏0, ✏0) . (3)

Because BPTD learns a single embedding of countries intocommunities, it preserves the traditional network-basednotion of community membership. Any sender–receiverasymmetry is captured by the core tensor ⇤, which we can


view as a compression of count tensor Y . By allowingon-diagonal elements, which we denote by �(r)

c �k and off-diagonal elements to be non-zero, the core tensor can rep-resent both within- and between-community interactions.

The elements of the core tensor are gamma-distributed,

�(r)c �k ⇠ �

�⌘ �c ⌘$c ⌫k⇢r, �

�(4)

�(r)

ck�!d

⇠ �(⌘$c ⌘$d ⌫k⇢r, �) c 6= d. (5)

Each community c 2 [C] has two positive weights ⌘ �

c

and ⌘$c that capture its rates of within- and between-community interaction, respectively. Each topic k 2 [K]has a positive weight ⌫k, while each regime r 2 [R] has apositive weight ⇢r. We place an uninformative prior overthe within-community interaction rates and gamma shrink-age priors over the other weights: ⌘ �

c ⇠ �(✏0, ✏0), ⌘$c ⇠�(�0 /C, ⇣), ⌫k ⇠ �(�0 /K, ⇣), and ⇢r ⇠ �(�0 /R, ⇣).These priors bias BPTD toward learning latent structurethat is sparse. Finally, we assume that � and ⇣ are drawnfrom an uninformative gamma prior: �, ⇣ ⇠ �(✏0, ✏0).

As K ! 1, the topic weights and their correspondingaction–topic factors constitute a draw GK =

P1k=1 ⌫k 1�k

from a gamma process (Ferguson, 1973). Similarly, asR ! 1, the regime weights and their correspond-ing time-step–regime factors constitute a draw GR =P1

r=1 ⇢r 1 rfrom another gamma process. As C ! 1,

the within- and between-community interaction weightsand their corresponding country–community factors con-stitute a draw GC =

P1c=1 ⌘

$c 1✓c from a marked gamma

process (Kingman, 1972). The mark associated with atom✓c = (✓1c, . . . , ✓Vc) is ⌘ �

c . We can view the elements ofthe core tensor and their corresponding factors as a drawG =

P1c=1

P1d=1

P1k=1

P1r=1 �

(r)

ck�!d

1✓c,✓d,�k, rfrom a

gamma process, provided that the expected sum of the coretensor elements is finite. This multirelational gamma pro-cess extends the relational gamma process of Zhou (2015).

Proposition 1: In the limit as C,K,R ! 1, the expectedsum of the core tensor elements is finite and equal to

E

2

41X

c=1

1X

k=1

1X

r=1

0

@�(r)c �k +

X

d 6=c

�(r)

ck�!d

1

A

3

5 =1

�

✓�30⇣3

+�40⇣4

◆.

We prove this proposition in the supplementary material.

3. Connections to Previous WorkPoisson CP decomposition: DuBois & Smyth (2010) de-veloped a model that assigns each event token (ignoringtime steps) to one of Q latent classes, where each class q 2[Q] is characterized by three categorical distributions—✓!q

over senders, ✓ q over receivers, and �q over actions—i.e.,

P (en=(ia�!j, t) | zn=q) = ✓!iq ✓

jq �aq. (6)

This model is closely related to the Poisson-based modelof Schein et al. (2015), which explicitly uses the canoni-cal polyadic (CP) tensor decomposition (Harshman, 1970)to factorize count tensor Y into four latent factor matrices.These factor matrices jointly embed senders, receivers, ac-tion types, and time steps into a Q-dimensional space,

y(t)

ia�!j

⇠ Po

QX

q=1

✓!iq ✓ jq �aq tq

!, (7)

where ✓!iq , ✓ jq , �aq , and tq are positive real numbers.

Schein et al.’s model generalizes Bayesian Poisson matrixfactorization (Cemgil, 2009; Gopalan et al., 2014; 2015;Zhou & Carin, 2015) and non-Bayesian Poisson CP de-composition (Chi & Kolda, 2012; Welling & Weber, 2001).

Although Schein et al.’s model is expressed in terms ofa tensor of event type counts, the relationship betweenthe multinomial and Poisson distributions (Kingman, 1972)means that we can also express it in terms of a set of eventtokens. This yields an equation that is similar to equation 6,

P (en=(ia�!j, t) | zn=q) / ✓!iq ✓

jq �aq tq. (8)

Conversely, DuBois & Smyth’s model can be expressedas a CP tensor decomposition. This equivalence is anal-ogous to the relationship between Poisson matrix factor-ization and latent Dirichlet allocation (Blei et al., 2003).

We can make Schein et al.’s model nonparametric byadding a per-class positive weight �q ⇠ �(�0

Q , ⇣), i.e.,

y(t)

ia�!j

⇠ Po

QX

q=1

✓!iq ✓ jq �aq tq �q

!. (9)

As Q ! 1 the per-class weights and their correspondinglatent factors constitute a draw from a gamma process.

Adding this per-class weight reveals that CP decomposi-tion is a special case of Tucker decomposition where thecardinalities of the latent dimensions are equal and the off-diagonal elements of the core tensor are zero. DuBois &Smyth’s and Schein et al.’s models are therefore highlyconstrained special cases of BPTD that cannot capturedimension-specific structure, such as communities of coun-tries or topics of action types. These models require eachlatent class to jointly summarize information about senders,receivers, action types, and time steps. This requirementconflates communities of countries and topics of actiontypes, thus forcing each class to capture potentially redun-dant information. Moreover, by definition, CP decompo-sition models cannot express between-community interac-tions and cannot express sender–receiver asymmetry with-out learning completely separate latent factor matrices for


senders and receivers. These limitations make it hard to in-terpret these models as learning community memberships.

Infinite relational models: The infinite relational model(IRM) of Kemp et al. (2006) also learns latent structurespecific to each dimension of an M -dimensional tensor;however, unlike BPTD, the elements of this tensor are bi-nary, indicating the presence or absence of the correspond-ing event type. The IRM therefore uses a Bernoulli like-lihood. Schmidt & Mørup (2013) extended the IRM tomodel a tensor of event counts by replacing the Bernoullilikelihood with a Poisson likelihood (and gamma priors):

y(t)

ia�!j

⇠ Po✓�(zt)

ziza�!zj

◆, (10)

where zi, zj 2 [C] are the respective community assign-ments of countries i and j, za 2 [K] is the topic as-signment of action a, and zt 2 [R] is the regime assign-ment of time step t. This model, which we refer to as thegamma–Poisson IRM (GPIRM), allocates M -dimensionalevent types to M -dimensional latent classes—e.g., it allo-cates all tokens of type (i

a�!j, t) to class (ziza�!zj , zt).

The GPIRM is a special case of BPTD where the rows ofthe latent factor matrices are constrained to be “one-hot”binary vectors—i.e., ✓ic = 1(zi = c), ✓jd = 1(zj = d),�ak=1(za=k), and tr=1(zt=r). With this constraint,the Poisson rates in equations 1 and 10 are equal. UnlikeBPTD, the GPIRM is a single-membership model. In ad-dition, it cannot express heterogeneity in rates of activityof the countries, action types, and time steps. The latterlimitation can be remedied by letting ✓izi , ✓jzj , �aza , and tzt be positive real numbers. We refer to this variant ofthe GPIRM as the degree-corrected GPIRM (DCGPIRM).

Stochastic block models: The IRM itself generalizesthe stochastic block model (SBM) of Nowicki & Sni-jders (2001), which learns latent structure from binary net-works. Although the SBM was originally specified using aBernoulli likelihood, Karrer & Newman (2011) introducedan alternative specification that uses the Poisson likelihood:

yi�!j ⇠ Po

CX

c=1

✓ic

CX

d=1

✓jd �c�!d

!, (11)

where ✓ic = 1(zi = c), ✓j = 1(zj = d), and �c�!d is apositive real number. Like the IRM and the GPIRM, theSBM is a single-membership model and cannot expressheterogeneity in the countries’ rates of activity. Airoldiet al. (2008) addressed the former limitation by letting✓ic 2 [0, 1] such that

PCc=1 ✓ic = 1. Meanwhile, Karrer

& Newman (2011) addressed the latter limitation by allow-ing both ✓izi and ✓jzj to be positive real numbers, muchlike the DCGPIRM. Ball et al. (2011) simultaneously ad-dressed both limitations by letting ✓ic, ✓jd � 0, but con-strained �c�!d = �d�!c. Finally, Zhou (2015) extended

Ball et al.’s model to be nonparametric and introduced thePoisson–Bernoulli distribution to link binary data to thePoisson likelihood in a principled fashion. In this model,the elements of the core matrix and their corresponding fac-tors constitute a draw from a relational gamma process.

Non-Poisson Tucker decomposition: Researchers some-times refer to the Poisson rate in equation 11 as be-ing “bilinear” because it can equivalently be written as✓j ⇤✓>i . Nickel et al. (2012) introduced RESCAL—a non-probabilistic bilinear model for binary data thatachieves state-of-the-art performance at relation extraction.Nickel et al. (2015) then introduced several extensions forextracting relations of different types. Bilinear models,such as RESCAL and its extensions, are all special cases(albeit non-probabilistic ones) of Tucker decomposition.

Hoff (2015) recently developed a Gaussian-based Tuckerdecomposition model and multilinear tensor regressionmodel (Hoff, 2014) for analyzing interaction event data.

Finally, there are many other Tucker decomposition meth-ods (Kolda & Bader, 2009). Although these include non-parametric (Xu et al., 2012) and nonnegative variants (Kim& Choi, 20007; Mørup et al., 2008; Cichocki et al., 2009),BPTD is the first such model to use a Poisson likelihood.

4. Posterior InferenceGiven an observed count tensor Y , inference in BPTD in-volves “inverting” the generative process to obtain the pos-terior distribution over the parameters conditioned on Yand hyperparameters ✏0 and �0. The posterior distributionis analytically intractable; however, we can approximateit using a set of posterior samples. We draw these sam-ples using Gibbs sampling, repeatedly resampling the valueof each parameter from its conditional posterior given Y ,✏0, �0, and the current values of the other parameters. Weexpress each parameter’s conditional posterior in a closedform using gamma–Poisson conjugacy and the auxiliaryvariable techniques of Zhou & Carin (2012). We providethe conditional posteriors in the supplementary material.

The conditional posteriors depend on Y via a set of “la-tent sources” (Cemgil, 2009) or subcounts. Because of thePoisson additivity theorem (Kingman, 1972), each latentsource y

(tr)

icak�!jd

is a Poisson-distributed random variable:

y(tr)

icak�!jd

⇠ Po✓✓ic ✓jd �ak tr �

(r)

ck�!d

◆(12)

y(t)

ia�!j

=CX

c=1

DX

d=1

KX

k=1

RX

r=1

y(tr)

icak�!jd

. (13)

Together, equations 12 and 13 are equivalent to equation 1.In practice, we can equivalently view each latent source in


terms of the token representation described in section 2,

y(tr)

icak�!jd

=NX

n=1

1(en=(ia�!j, t))1(zn=(c

k�!d, r)), (14)

where each token’s class assignment zn is an auxiliary la-tent variable. Using this representation, computing the la-tent sources (given the current values of the model param-eters) simply involves allocating event tokens to classes,much like the inference algorithm for DuBois & Smyth’smodel, and aggregating them using equation 14. The con-ditional posterior for each token’s class assignment is

P (zn=(ck�!d, r) | en=(i

a�!j, t),Y , ✏0, �0, . . .)

/ ✓ic ✓jd �ak tr �(r)

ck�!d

. (15)

Computation is dominated by the normalizing constant

Z(t)

ia�!j

=CX

c=1

CX

d=1

KX

k=1

RX

r=1

✓ic ✓jd �ak tr �(r)

ck�!d

. (16)

Computing this normalizing constant naıvely involvesO(C ⇥ C ⇥ K ⇥ R) operations; however, because eachlatent class (c k�!d, r) is composed of four separate dimen-sions, we can improve efficiency. We instead compute

Z(t)

ia�!j

=CX

c=1

✓ic

CX

d=1

✓jd

KX

k=1

✓ak

RX

r=1

tr �(r)

ck�!d

, (17)

which involves O(C + C +K +R) operations.

Compositional allocation using equations 15 and 17 im-proves computational efficiency significantly over naıvenon-compositional allocation using equations 15 and 16. Inpractice, we set C, K, and R to large values to approximatethe nonparametric interpretation of BPTD. If, for example,C = 50, K = 10, and R = 5, computing the normalizingconstant for equation 15 using equation 16 requires 2,753times the number of operations implied by equation 17.

Proposition 2: For an M -dimensional core tensor withD1 ⇥ . . .⇥DM elements, computing the normalizing con-stant using non-compositional allocation requires 1 ⇡ <1 times the number of operations required to compute itusing compositional allocation. When D1= . . .=DM =1,⇡=1. As Dm, Dm0 ! 1 for any m and m0 6=m, ⇡ ! 1.

We prove this proposition in the supplementary material.

BPTD and other Poisson-based models yield allocation in-ference algorithms that take advantage of the inherent spar-sity of the data and scale with the number of event to-kens. In contrast, non-Poisson tensor decomposition mod-els (including Hoff’s model) lead to algorithms that scalewith the size of the count tensor. Allocation-based infer-ence in BPTD is especially efficient because it composi-tionally allocates each M -dimensional event token to an

V

V

A

K

C

C

Figure 2. Compositional allocation. For clarity, we show the allo-cation process for a three-dimensional count tensor (ignoring timesteps). Observed three-dimensional event tokens (left) are com-positionally allocated to three-dimensional latent classes (right).

M -dimensional latent class. Figure 2 illustrates this pro-cess. CP decomposition models, such as those of DuBois& Smyth (2010) and Schein et al. (2015), only permit non-compositional allocation. For example, while BPTD allo-cates each token en = (i

a�!j, t) to a four-dimensional la-tent class (c k�!d, r), Schein et al.’s model allocates en to aone-dimensional latent class q that cannot be decomposed.Therefore, when Q=C⇥C⇥K⇥R, BPTD yields a fasterallocation inference algorithm than Schein et al.’s model.

5. Country–Country Interaction Event DataOur data come from the Integrated Crisis Early Warn-ing System (ICEWS) of Boschee et al. and the GlobalDatabase of Events, Language, and Tone (GDELT) of Lee-taru & Schrodt (2013). ICEWS and GDELT both use theConflict and Mediation Event Observations (CAMEO) hi-erarchy (Gerner et al.) for senders, receivers, and actions.

The top-level CAMEO coding for senders and receiversis their country affiliation, while lower levels in the hier-archy incorporate more specific attributes like their sec-tors (e.g., government or civilian) and their religious orethnic affiliations. When studying international relationsusing CAMEO-coded event data, researchers usually con-sider only the senders’ and receivers’ countries. There are249 countries represented in ICEWS, which include non-universally recognized states, such as Occupied PalestinianTerritory, and former states, such as Former Yugoslav Re-public of Macedonia; there are 233 countries in GDELT.

The top level for actions, which we use in our analyses,consists of twenty action classes, roughly ranked accordingto their overall sentiment. For example, the most negative is20—Use Unconventional Mass Violence. CAMEO furtherdivides these actions into the QuadClass scheme: VerbalCooperation (actions 2–5), Material Cooperation (actions6–7), Verbal Conflict (actions 8–16), and Material Conflict(16–20). The first action (1—Make Statement) is neutral.


6. Predictive AnalysisBaseline models: We compared BPTD’s predictive perfor-mance to that of three baseline models, described in sec-tion 3: 1) GPIRM, 2) DCGPIRM, and 3) the BayesianPoisson tensor factorization (BPTF) model of Schein et al.(2015). All three models use a Poisson likelihood and havethe same two hyperparameters as BPTD—i.e., ✏0 and �0.We set ✏0 to 0.1, as recommended by Gelman (2006), andwe set �0 so that (�0 /C)2 (�0 /K) (�0 /R) = 0.01. Thisparameterization encourages the elements of the core ten-sor ⇤ to be sparse. We implemented an MCMC inferencealgorithm for each model. We provide the full generativeprocess for all three models in the supplementary material.

GPIRM and DCGPIRM are both Tucker decompositionmodels and thus allocate events to four-dimensional la-tent classes. The cardinalities of these latent dimensionsare the same as BPTD’s—i.e., C, K, and R. In con-trast, BPTF is a CP decomposition model and thus allo-cates events to one-dimensional latent classes. We set thecardinality of this dimension so that the total number oflatent factors in BPTF’s likelihood was equal to the to-tal number of latent factors in BPTD’s likelihood—i.e.,Q = d (V⇥C)+(A⇥K)+(T⇥R)+(C2⇥K⇥R)

V+V+A+T+1 e. We chose notto let BPTF and BPTD use the same number of latentclasses—i.e., to set Q = C2 ⇥ K ⇥ R. BPTF does notpermit non-compositional allocation, so MCMC inferencebecomes very slow for even moderate values of C, K, andR. CP decomposition models also tend to overfit when Qis large (Zhao et al., 2015). Throughout our predictive ex-periments, we let C=20, K=6, and R=3. These valueswere well-supported by the data, as we explain in section 7.

Experimental setup: We constructed twelve different ob-served tensors—six from ICEWS and six from GDELT.Five of the six tensors for each source (ICEWS or GDELT)correspond to one-year time spans with monthly time steps,starting with 2004 and ending with 2008; the sixth corre-sponds to a five-year time span with monthly time steps,spanning 1995–2000. We divided each tensor Y into atraining tensor Y train = Y (1), . . . ,Y (T�3) and a test ten-sor Y test = Y (T�2), . . . ,Y (T ). We further divided eachtest tensor into a held-out portion and an observed por-tion via a binary mask. We experimented with two dif-ferent masks: one that treats the elements involving themost active fifteen countries as the held-out portion and theremaining elements as the observed portion, and one thatdoes the opposite. The first mask enabled us to evaluatethe models’ reconstructions of the densest (and arguablymost interesting) portion of each test tensor, while the sec-ond mask enabled us to evaluate their reconstructions ofits complement. Across the entire GDELT database, forexample, the elements involving the most active fifteencountries—i.e., 6% of all 233 countries—account for 30%

of the event tokens. Moreover, 40% of these elements arenon-zero. These non-zero elements are highly dispersed,with a variance-to-mean ratio of 220. In contrast, only0.7% of the elements involving the other countries are non-zero. These elements have a variance-to-mean ratio of 26.

For each combination of the four models, twelve tensors,and two masks, we ran 5,000 iterations of MCMC inferenceon the training tensor. We clamped the country–communityfactors, the action–topic factors, and the core tensor andthen inferred the time-step–regime factors for the test ten-sor using its observed portion by running 1,000 iterations ofMCMC inference. We saved every tenth sample after thefirst 500. We used each sample, along with the country–community factors, the action–topic factors, and the coretensor, to compute the Poisson rate for each element in theheld-out portion of the test tensor. Finally, we averagedthese rates across samples and used each element’s aver-age rate to compute its probability. We combined the held-out elements’ probabilities by taking their geometric meanor, equivalently, by computing their inverse perplexity. Wechose this combination strategy to ensure that the modelswere penalized heavily for making poor predictions on thenon-zero elements and were not rewarded excessively formaking good predictions on the zero elements. By clamp-ing the country–community factors, the action–topic fac-tors, and the core tensor after training, our experimentalsetup is analogous to that used to assess collaborative fil-tering models’ strong generalization ability (Marlin, 2004).

Results: Figure 3 illustrates the results for each combi-nation of the four models, twelve tensors, and two masks.The top row contains the results from the twelve experi-ments involving the first mask, where the elements involv-ing the most active fifteen countries were treated as theheld-out portion. BPTD outperformed the baselines signif-icantly. BPTF—itself a state-of-the-art model—performedbetter than BPTD in only one experiment. In general, theTucker decomposition allows BPTD to learn richer latentstructure that generalizes better to held-out data. The bot-tom row contains the results from the experiments involv-ing the second mask. The models’ performance was closerin these experiments, probably because of the large pro-portion of easy-to-predict zero elements. BPTD and BPTFperformed indistinguishably in these experiments, and bothmodels outperformed the GPIRM and the DCGPIRM. Thesingle-membership nature of the GPIRM and the DCG-PIRM prevents them from expressing high levels of hetero-geneity in the countries’ rates of activity. When the held-out elements were highly dispersed, these models some-times made extremely inaccurate predictions. In contrast,the mixed-membership nature of BPTD and BPTF allowsthem to better express heterogeneous rates of activity.


0.0

0.5

1.0 3.9e-033.9e-033.9e-033.9e-03

GDELT1995-2000

3.3e-023.3e-023.3e-023.3e-02

ICEWS1995-2000

6.4e-046.4e-046.4e-046.4e-04

GDELT2004

4.9e-024.9e-024.9e-024.9e-02

ICEWS2004

1.1e-021.1e-021.1e-021.1e-02

GDELT2005

2.6e-022.6e-022.6e-022.6e-02

ICEWS2005

1.2e-041.2e-041.2e-041.2e-04

GDELT2006

gpirmdcgpirmbptfbptd

1.7e-021.7e-021.7e-021.7e-02

ICEWS2006

1.4e-061.4e-061.4e-061.4e-06

GDELT2007

1.2e-021.2e-021.2e-021.2e-02

ICEWS2007

7.7e-077.7e-077.7e-077.7e-07

GDELT2008

3.1e-023.1e-023.1e-023.1e-02

ICEWS2008

0.0

0.5

1.0 9.1e-019.1e-019.1e-019.1e-01 9.8e-019.8e-019.8e-019.8e-01 8.4e-018.4e-018.4e-018.4e-01 9.5e-019.5e-019.5e-019.5e-01 8.8e-018.8e-018.8e-018.8e-01 9.5e-019.5e-019.5e-019.5e-01 8.6e-018.6e-018.6e-018.6e-01 9.4e-019.4e-019.4e-019.4e-01 8.0e-018.0e-018.0e-018.0e-01 9.4e-019.4e-019.4e-019.4e-01 7.1e-017.1e-017.1e-017.1e-01 9.3e-019.3e-019.3e-019.3e-01

Figure 3. Predictive performance. Each plot shows the inverse perplexity (higher is better) for the four models: the GPIRM (blue), theDCGPIRM (green), BPTF (red), and BPTD (yellow). In the experiments depicted in the top row, we treated the elements involving themost active countries as the held-out portion; in the experiments depicted in the bottom row, we treated the remaining elements as theheld-out portion. For ease of comparison, we scaled the inverse perplexities to lie between zero and one; we give the scales in the top-leftcorners of the plots. BPTD outperformed the baselines significantly when predicting the denser portion of each test tensor (top row).

7. Exploratory AnalysisWe used a tensor of ICEWS events spanning 1995–2000,with monthly time steps, to explore the latent structure dis-covered by BPTD. We initially let C = 50, K = 8, andR= 3—i.e., C ⇥ C ⇥ K ⇥ R = 60, 000 latent classes—and used the shrinkage priors to adaptively learn the mostappropriate numbers of communities, topics, and regimes.We found C = 20 communities and K = 6 topics withweights that were significantly greater than zero. We pro-vide a plot of the community weights in the supplementarymaterial. Although all three regimes had non-zero weights,one had a much larger weight than the other two. Forcomparison, Schein et al. (2015) used fifty latent classesto model the same data, while Hoff (2015) used C = 4,K=4, and R=4 to model a similar tensor from GDELT.

Topics of action types: We show the inferred action–topicfactors as a heatmap in the left subplot of figure 4. Weordered the topics by their weights ⌫1, . . . , ⌫K , which areabove the heatmap. The inferred topics correspond veryclosely to CAMEO’s QuadClass scheme. Moving from leftto right, the topics place their mass on increasingly nega-tive actions. Topics 1 and 2 place most of their mass onVerbal Cooperation actions; topic 3 places most of its masson Material Cooperation actions and the neutral 1—MakeStatement action; topic 4 places most of its mass on Ver-bal Conflict actions and the 1—Make Statement action; andtopics 5 and 6 place their mass on Material Conflict actions.

Topic-partitioned community–community networks: Inthe right subplot of figure 4, we visualize the inferred com-munity structure for topic k=1 and the most active regimer. The bottom-left heatmap is the community–communityinteraction network ⇤(r)

k . The top-left heatmap depicts therate at which each country i acts as a sender in each com-munity c—i.e., ✓ic

PVj=1

PCd=1 ✓jd �

(r)

ck�!d

. Similarly, thebottom-right heatmap depicts the rate at which each coun-try acts as a receiver in each community. The top-rightheatmap depicts the number of times each country i took

an action associated with topic k toward each country j

during regime r—i.e.,PC

c=1

PCd=1

PAa=1

PTt=1 y

(tr)

icak�!jd

.

We grouped the countries by their strongest communitymemberships and ordered the communities by their within-community interaction weights ⌘ �

1 , . . . , ⌘ �

C , from smallestto largest; the thin green lines separate the countries that arestrongly associated with one community from the countriesthat are strongly associated with its adjacent communities.

Some communities contain only one or two strongly as-sociated countries. For example, community 1 containsonly the US, community 6 contains only China, and com-munity 7 contains only Russia and Belarus. These com-munities mostly engage in between-community interac-tion. Other larger communities, such as communities 9and 15, mostly engage in within-community interaction.Most communities have a strong geographic interpreta-tion. Moving upward from the bottom, there are com-munities that correspond to Eastern Europe, East Africa,South-Central Africa, Latin America, Australasia, CentralEurope, Central Asia, etc. The community–community in-teraction network summarizes the patterns in the top-rightheatmap. This topic is dominated by the 4–Consult action,so the network is symmetric; the more negative topics haveasymmetric community–community interaction networks.We therefore hypothesize that cooperation is an inherentlyreciprocal type of interaction. We provide visualizationsfor the other five topics in the supplementary material.

8. SummaryWe presented Bayesian Poisson Tucker decomposition(BPTD) for learning the latent structure of international re-lations from country–country interaction events of the form“country i took action a toward country j at time t.” Unlikeprevious models, BPTD takes advantage of all three repre-sentations of an interaction event data set: 1) a set of eventtokens, 2) a tensor of event type counts, and 3) a series ofweighted multinetwork snapshots. BPTD uses a Poisson


1 2 3 4 5 6

Engage inMass Violence

Fight

Assault

Coerce

ReduceRelations

Posture

Protest

Threaten

Reject

Disapprove

Demand

Investigate

Yield

Aid

Cooperate(Material)

Cooperate(Diplomatic)

Consult

Intend toCooperate

Appeal

MakeStatement

0.0

0.5

1.0

1.5

2.0

2.5

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

2019

1817

1615

1413

1211

109

87

65

43

21

UkraineGeorgia

AzerbaijanArmenia

SudanEthiopiaSomalia

LibyaKenyaSouth Africa

NigeriaUgandaZimbabweCanadaSpain

CubaMexico

ColombiaChile

ArgentinaBrazil

VenezuelaPeru

PortugalNew ZealandAustralia

IndonesiaSwitzerland

ItalyHoly SeeGermanyNetherlandsBulgariaBelgium

LithuaniaLatvia

RomaniaPolandAustria

Czech Rep.SlovakiaHungaryIran

KazakhstanUzbekistanKyrgyzstanAfghanistan

TajikistanTaiwan

SingaporePhilippinesMalaysiaVietnamThailand

CambodiaMyanmarMacedonia

TurkeyGreeceCyprusPalestine

LebanonIsrael

FranceKuwaitYemenAlgeria

Saudi ArabiaSyria

EgyptJordanJapan

North KoreaSouth Korea

BelarusRussiaChina

BangladeshPakistanSri Lanka

IndiaIraq

CroatiaAlbaniaBosniaKosovoSerbiaIreland

UKUSA

USA U

KIre

land

Serb

iaK

osov

oB

osni

aA

lban

iaC

roat

iaIra

qIn

dia

Sri L

anka

Paki

stan

Ban

glad

esh

Chi

naR

ussi

aB

elar

usSo

uth

Kor

eaN

orth

Kor

eaJa

pan

Jord

anEg

ypt

Syria

Saud

i Ara

bia

Alg

eria

Yem

enK

uwai

tFr

ance

Isra

elLe

bano

nPa

lest

ine

Cyp

rus

Gre

ece

Turk

eyM

aced

onia

Mya

nmar

Cam

bodi

aTh

aila

ndVi

etna

mM

alay

sia

Phili

ppin

esSi

ngap

ore

Taiw

anTa

jikis

tan

Afg

hani

stan

Kyr

gyzs

tan

Uzb

ekis

tan

Kaz

akhs

tan

Iran

Hun

gary

Slov

akia

Cze

ch R

ep.

Aus

tria

Pola

ndR

oman

iaLa

tvia

Lith

uani

aB

elgi

umB

ulga

riaN

ethe

rland

sG

erm

any

Hol

y Se

eIta

lySw

itzer

land

Indo

nesi

aA

ustr

alia

New

Zea

land

Port

ugal

Peru

Vene

zuel

aB

razi

lA

rgen

tina

Chi

leC

olom

bia

Mex

ico

Cub

aSp

ain

Can

ada

Zim

babw

eU

gand

aN

iger

iaSo

uth

Afr

ica

Ken

yaLi

bya

Som

alia

Ethi

opia

Suda

nA

rmen

iaA

zerb

aija

nG

eorg

iaU

krai

ne

Figure 4. Left: Action–topic factors. The topics are ordered by ⌫1, . . . , ⌫K (above the heatmap). Right: Latent structure discovered byBPTD for topic k = 1 and the most active regime, including the community–community interaction network (bottom left), the rate atwhich each country acts as a sender (top left) and a receiver (bottom right) in each community, and the number of times each country itook an action associated with topic k toward each country j during regime r (top right). We show only the most active 100 countries.

likelihood, respecting the discrete nature of the data and itsinherent sparsity. Moreover, BPTD yields a compositionalallocation inference algorithm that is more efficient thannon-compositional allocation algorithms. Because BPTDis a Tucker decomposition model, it shares parametersacross latent classes. In contrast, CP decomposition mod-els force each latent class to capture potentially redundantinformation. BPTD therefore “does more with less.” Thisefficiency is reflected in our predictive analysis: BPTD out-performs BPTF—a CP decomposition model—as well astwo other baselines. BPTD learns interpretable latent struc-ture that aligns with well-known concepts from the net-works literature. Specifically, BPTD learns latent country–community memberships, including the number of com-munities, as well as directed community–community inter-action networks that are specific to topics of action typesand temporal regimes. This structure captures the complex-

ity of country–country interactions, while revealing pat-terns that agree with our knowledge of international rela-tions. Finally, although we presented BPTD in the contextof interaction events, BPTD is well suited to learning latentstructure from other types of multidimensional count data.

AcknowledgementsWe thank Abigail Jacobs and Brandon Stewart for help-ful discussions. This work was supported by NSF #SBE-0965436, #IIS-1247664, #IIS-1320219; ONR #N00014-11-1-0651; DARPA #FA8750-14-2-0009, #N66001-15-C-4032; Adobe; the John Templeton Foundation; the SloanFoundation; the UMass Amherst Center for Intelligent In-formation Retrieval. Any opinions, findings, conclusions,or recommendations expressed in this material are the au-thors’ and do not necessarily reflect those of the sponsors.


ReferencesAiroldi, E. M., Blei, D. M., Feinberg, S. E., and Xing, E. P.

Mixed membership stochastic blockmodels. Journal ofMachine Learning Research, 9:1981–2014, 2008.

Ball, B., Karrer, B., and Newman, M. E. J. Efficientand principled method for detecting communities in net-works. Physical Review E, 84(3), 2011.

Blei, D., Ng, A., and Jordan, M. Latent Dirichlet allo-cation. Journal of Machine Learning Research, 3:993–1022, 2003.

Boschee, E., Lautenschlager, J., O’Brien, S., Shellman, S.,Starz, J., and Ward, M. ICEWS coded event data. Har-vard Dataverse. V10.

Cemgil, A. T. Bayesian inference for nonnegative matrixfactorisation models. Computational Intelligence andNeuroscience, 2009.

Chi, E. C. and Kolda, T. G. On tensors, sparsity, and non-negative factorizations. SIAM Journal on Matrix Analy-sis and Applications, 33(4):1272–1299, 2012.

Cichocki, A., Zdunek, R., Phan, A. H., and i Amari, S.Nonnegative Matrix and Tensor Factorizations: Appli-cations to Exploratory Multi-Way Data Analysis andBlind Source Separation. John Wiley & Sons, 2009.

DuBois, C. and Smyth, P. Modeling relational events vialatent classes. In Proceedings of the Sixteenth ACMSIGKDD International Conference on Knowledge Dis-covery and Data Mining, pp. 803–812, 2010.

Ferguson, T. S. A Bayesian analysis of some nonparametricproblems. The Annals of Statistics, 1(2):209–230, 1973.

Gelman, A. Prior distributions for variance parameters inhierarchical models. Bayesian Analysis, 1(3):515–533,2006.

Gerner, D. J., Schrodt, P. A., Abu-Jabr, R., and Yilmaz, O.Conflict and mediation event observations (CAMEO): Anew event data framework for the analysis of foreign pol-icy interactions. Working paper.

Gopalan, P., Ruiz, F. J. R., Ranganath, R., and Blei,D. M. Bayesian nonparametric Poisson factorization forrecommendation systems. In Proceedings of the Sev-enteenth International Conference on Artificial Intelli-gence and Statistics, volume 33, pp. 275–283, 2014.

Gopalan, P., Hofman, J., and Blei, D. Scalable recommen-dation with Poisson factorization. In Proceedings of theThirty-First Conference on Uncertainty in Artificial In-telligence, 2015.

Harshman, R. Foundations of the PARAFAC procedure:Models and conditions for an “explanatory” multimodalfactor analysis. UCLA Working Papers in Phonetics, 16:1–84, 1970.

Hoff, P. Multilinear tensor regression for longitudinal rela-tional data. arXiv:1412.0048, 2014.

Hoff, P. Equivariant and scale-free Tucker decompositionmodels. Bayesian Analysis, 2015.

Karrer, B. and Newman, M. E. J. Stochastic blockmodelsand community structure in networks. Physical ReviewE, 83(1), 2011.

Kemp, C., Tenenbaum, J. B., Griffiths, T. L., Yamada, T.,and Ueda, N. Learning systems of concepts with an infi-nite relational model. In Proceedings of the Twenty-FirstNational Conference on Artificial Intelligence, 2006.

Kim, Y.-D. and Choi, S. Nonnegative Tucker decomposi-tion. In Proceedings of the IEEE Conference on Com-puter Vision and Pattern Recognition, 20007.

Kingman, J. F. C. Poisson Processes. Oxford UniversityPress, 1972.

Kolda, T. G. and Bader, B. W. Tensor decompositions andapplications. SIAM Review, 51(3):455–500, 2009.

Leetaru, K. and Schrodt, P. GDELT: Global data on events,location, and tone, 1979–2012. Working paper, 2013.

Marlin, B. Collaborative filtering: A machine learning per-spective. Master’s thesis, University of Toronto, 2004.

Mørup, M., Hansen, L. K., and Arnfred, S. M. Algorithmsfor sparse nonnegative Tucker decompositions. NeuralComputation, 20(8):2112–2131, 2008.

Nickel, M., Tresp, V., and Kriegel, H.-P. FactorizingYAGO: Scalable machine learning for linked data. InProceedings of the Twenty-First International WorldWide Web Conference, pp. 271–280, 2012.

Nickel, M., Murphy, K., Tresp, V., and Gabrilovich,E. A review of relational machine learning forknowledge graphs: From multi-relational link pre-diction to automated knowledge graph construction.arXiv:1503.00759, 2015.

Nowicki, K. and Snijders, T. A. B. Estimation and predic-tion for stochastic blockstructures. Journal of the Amer-ican Statistical Association, 96(455):1077–1087, 2001.

Schein, A., Paisley, J., Blei, D. M., and Wallach, H.Bayesian Poisson tensor factorization for inferrring mul-tilateral relations from sparse dyadic event counts. In


Proceedings of the Twenty-First ACM SIGKDD Inter-national Conference on Knowledge Discovery and DataMining, pp. 1045–1054, 2015.

Schmidt, M. N. and Mørup, M. Nonparametric Bayesianmodeling of complex networks: An introduction. IEEESignal Processing Magazine, 30(3):110–128, 2013.

Tucker, L. R. The extension of factor analysis to three-dimensional matrices. In Frederiksen, N. and Gullik-sen, H. (eds.), Contributions to Mathematical Psychol-ogy. Holt, Rinehart and Winston, 1964.

Welling, M. and Weber, M. Positive tensor factorization.Pattern Recognition Letters, 22(12):1255–1261, 2001.

Xu, Z., Yan, F., and Qi, Y. Infinite Tucker decomposition:Nonparametric Bayesian models for multiway data anal-ysis. In Proceedings of the Twenty-Ninth InternationalConference on Machine Learning, pp. 1023–1030, 2012.

Zhao, Q., Zhang, L., and Cichocki, A. Bayesian CP fac-torization of incomplete tensors with automatic rank de-termination. IEEE Transactions on Pattern Analysis andMachine Intelligence, 37(9):1751–1763, 2015.

Zhou, M. Infinite edge partition models for overlappingcommunity detection and link prediction. In Proceed-ings of the Eighteenth International Conference on Arti-ficial Intelligence and Statistics, pp. 1135–1143, 2015.

Zhou, M. and Carin, L. Augment-and-conquer negativebinomial processes. In Advances in Neural InformationProcessing Systems Twenty-Five, pp. 2546–2554, 2012.

Zhou, M. and Carin, L. Negative binomial process countand mixture modeling. IEEE Transactions on Pat-tern Analysis and Machine Intelligence, 37(2):307–320,2015.

Supplementary Material for“Bayesian Poisson Tucker Decomposition for Learning

the Structure of International Relations”

Proceedings of the 33 rdInternational Conference on Machine Learning, New York, NY, USA, 2016.

JMLR: W&CP volume 48. Copyright 2016 by the author(s).

Aaron Schein Mingyuan Zhou David M. Blei Hanna Wallach

1

1 Proposition 1

In the limit as C,K,R ! 1, the expected sum of the core tensor elements is finite and equal to

E

2

41X

c=1

1X

k=1

1X

r=1

0

@�

(r)c �k +

X

d 6=c

�

(r)

ck�!d

1

A

3

5 =1

�

✓�

30

⇣

3+

�

40

⇣

4

◆.

The proof is very similar to that of Zhou (2015, Lemma 1). By the law of total expectation,

E

2

41X

c=1

1X

k=1

1X

r=1

0

@�

(r)c �k +

X

d 6=c

�

(r)

ck�!d

1

A

3

5 =1X

c=1

1X

k=1

1X

r=1

0

@Eh�

(r)c �ki+X

d 6=c

E�

(r)

ck�!d

�1

A

=1X

c=1

1X

k=1

1X

r=1

0

@E⌘

�

c ⌘

$c ⌫k⇢r

�

�+X

d 6=c

E⌘

$c ⌘

$d ⌫k⇢r

�

�1

A

=1

�

1X

c=1

1X

k=1

1X

r=1

0

@E⇥⌘

�

c ⌘

$c ⌫k⇢r

⇤+X

d 6=c

E [⌘$c ⌘

$d ⌫k⇢r]

1

A

=1

�

E" 1X

k=1

⌫k

#E" 1X

r=1

⇢r

# 1X

c=1

0

@E⇥⌘

�

c ⌘

$c

⇤+X

d 6=c

E [⌘$c ⌘

$d ]

1

A

=1

�

✓�0

⇣

◆✓�0

⇣

◆ 1X

c=1

0

@E⇥⌘

�

c ⌘

$c

⇤+X

d 6=c

E [⌘$c ⌘

$d ]

1

A

=1

�

✓�0

⇣

◆20

@1X

c=1

E⇥⌘

�

c

⇤E [⌘$c ] + E

2

41X

c=1

X

d 6=c

⌘

$c ⌘

$d

3

5

1

A.

The marks ⌘ �

c are gamma distributed with mean 1, so

=1

�

✓�0

⇣

◆20

@E" 1X

c=1

⌘

$c

#+ E

2

41X

c=1

X

d 6=c

⌘

$c ⌘

$d

3

5

1

A

=1

�

✓�0

⇣

◆20

@�0

⇣

+ E

2

41X

c=1

X

d 6=c

⌘

$c ⌘

$d

3

5

1

A

=1

�

✓�0

⇣

◆2 �0

⇣

+ E" 1X

c=1

1X

d=1

⌘

$c ⌘

$d

#� E

" 1X

c=1

⌘

$c ⌘

$c

#!

=1

�

✓�0

⇣

◆2 �0

⇣

+ E" 1X

c=1

⌘

$c

! 1X

d=1

⌘

$d

!#� E

" 1X

c=1

⌘

$c ⌘

$c

#!.

2

Using E [(P1

c=1 ⌘$c ) (

P1d=1 ⌘

$d )] = �2

0⇣2 + �0

⇣2 , we can write

=1

�

✓�0

⇣

◆2 �0

⇣

+�

20

⇣

2+

�0

⇣

2� E

" 1X

c=1

⌘

$c ⌘

$c

#!.

Finally, using Campbell’s Theorem (Kingman, 1972), we know that E [P1

c=1 ⌘$c ⌘

$c ] = �0

⇣2 , so

=1

�

✓�0

⇣

◆2✓�0

⇣

+�

20

⇣

2+

�0

⇣

2� �0

⇣

2

◆

=1

�

✓�0

⇣

◆2✓�0

⇣

+�

20

⇣

2

◆

=1

�

✓�

30

⇣

3+

�

40

⇣

4

◆.

2 Proposition 2

For an M -dimensional core tensor with D1⇥. . .⇥DM elements, computing the normalizing constant using

non-compositional allocation requires 1 ⇡ < 1 times the number of operations required by compositional

allocation. When D1= . . .=DM =1, ⇡=1. As Dm, Dm0 ! 1 for any m and m

0 6=m, ⇡ ! 1.

Each event token occurs in an M -dimensional discrete coordinate space—i.e., en = p, where p =(p1, . . . , pM ) is a multi-index. Similarly, each event token’s latent class assignment also occurs inan M -dimensional discrete coordinate space—i.e., zn=q, where q = (q1, . . . , qM ) is a multi-index.

Assuming M factor matrices ⇥(1), . . . ,⇥(M) and an M -dimensional core tensor ⇤,

P (zn=q | en=p) / �q

MY

m=1

✓

(m)pmqm .

The computational bottleneck in MCMC inference is computing the normalizing constant

Zp =X

q

�q

MY

m=1

✓

(m)pmqm .

If we use a naıve non-compositional approach, then (assuming each latent dimension m has car-dinality Dm) the sum over q involves

QMm=1 Dm terms and each term requires M multiplications.

Thus, computing Zp requires a total of MQM

m=1 Dm multiplications andQM

m=1 Dm additions.1

However, we can also compute Zp using a compositional approach—i.e.,

Zp =D1X

q1=1

✓

(1)p1q1

D2X

q2=1

✓

(2)p2q2 . . .

DMX

qM=1

✓

(M)pMqM �q.

1Computing a sum of N terms requires either N or N � 1 additions, depending on whether or not you add the firstterm to zero. We assume the former definition and say that computing a sum of N terms requires N additions.

3

This approach requires a total ofPM

m=1 Dm multiplications and 1 +PM

m=1(Dm � 1) additions.

The ratio ⇡ of the number of operations (i.e., multiplications and additions) required by the non-compositional approach to the number of operations required by the compositional approach is

⇡ =

⇣M

QMm=1 Dm

⌘+⇣QM

m=1 Dm

⌘

⇣PMm=1 Dm

⌘+⇣1 +

PMm=1(Dm�1)

⌘

=(M+1)

QMm=1 Dm⇣

2PM

m=1 Dm

⌘�M + 1

.

As the cardinalities D1, . . . , DM of the latent dimensions grow, the numerator grows at a fasterrate than the denominator. Therefore ⇡ achieves its lower bound when D1 = . . . = DM = 1:

⌦(⇡) =(M + 1)

(2M)�M + 1.

Because the numerator grows at a faster rate than the denominator, we can find the upper boundby taking the limit as one or more cardinalities tend to infinity. We work with the inverse ratio

⇡

�1 =

⇣2PM

m=1 Dm

⌘�M + 1

(M + 1)QM

m=1 Dm

=2

M + 1

MX

m=1

DmQMm=1 Dm

!� M � 1

M + 1

1

QMm=1 Dm

!

=2

M + 1

MX

m=1

1Qm0 6=m Dm0

!� M � 1

M + 1

1

QMm=1 Dm

!.

First, we take the limit of ⇡�1 as a single cardinality Dm ! 1:

limDm!1

⇡

�1 = limDm!1

2

M + 1

MX

m=1

1Qn 6=m Dn

!� lim

Dm!1

M � 1

M + 1

1

QMm=1 Dm

!

= limDm!1

2

M + 1

MX

m=1

1Qn 6=m Dn

!

=2

M + 1

1Q

n 6=m Dn

!.

However, as any second cardinality Dm0 ! 1,

limDm,Dm0!1

⇡

�1 = limDm0!1

2

M + 1

1Q

n 6=m Dn

!! 0.

Therefore, ⇡ ! 1 as any two (or more) cardinalities tend to infinity.

4

3 Inference

Gibbs sampling repeatedly resamples the value of each latent variable from its conditional poste-rior. In this section, we provide the conditional posterior for each latent variable in BPTD.

We start by defining the Chinese restaurant table (CRT) distribution (Zhou & Carin, 2015): If l ⇠CRT(m, r) is a CRT-distributed random variable, then, we can equivalently say that

l ⇠mX

n=1

Bern✓

r

r + n� 1

◆.

We also define g(x) ⌘ ln(1 + x).

Throughout this section, we use, e.g., (✓ic |�) to denote ✓ic conditioned on Y , ✏0, �0, and thecurrent values of the other latent variables. We assume that Y is partially observed and include abinary mask B, where b

(t)

ia�!j

=0 means that y(t)i

a�!j=0 is unobserved, not an observed zero.

Action–Topic Factors:

y

(·)·ak$·

⌘VX

i=1

CX

c=1

X

j 6=i

CX

d=1

TX

t=1

RX

r=1

y

(tr)

icak�!dj

⇠ak ⌘VX

i=1

X

j 6=i

TX

t=1

b

(t)

ia�!j

CX

c=1

✓ic

CX

d=1

✓jd

RX

r=1

tr �(r)

ck�!d

(�ak |�) ⇠ �⇣✏0 + y

(·)·ak$·

, ✏0 + ⇠ak

⌘

Time-Step–Regime Factors:

y

(tr)

··�!·

⌘VX

i=1

CX

c=1

X

j 6=i

CX

d=1

AX

a=1

KX

k=1

y

(tr)

icak�!dj

⇠tr ⌘VX

i=1

X

j 6=i

AX

a=1

b

(t)

ia�!j

CX

c=1

✓ic

CX

d=1

✓jd

KX

k=1

�ak �(r)

ck�!d

( tr |�) ⇠ �⇣✏0 + y

(tr)

··�!·, ✏0 + ⇠tr

⌘

5

Country–Community Factors:

y

(·)ic

·$·⌘X

j 6=i

CX

d=1

AX

a=1

KX

k=1

TX

t=1

RX

r=1

✓y

(tr)

icak�!dj

+ y

(tr)

jdak�!ci

◆

⇠ic ⌘X

j 6=i

AX

a=1

TX

t=1

b

(t)

ia�!j

CX

d=1

✓jd

KX

k=1

�ak

RX

r=1

tr �(r)

ck�!d

+ b

(t)

ja�!i

CX

d=1

✓jd

KX

k=1

�ak

RX

r=1

tr �(r)

dk�!c

!

(✓ic |�) ⇠ �⇣↵i + y

(·)ic

·$·,�i + ⇠ic

⌘

Auxiliary Latent Country–Community Counts:

(`ic |�) ⇠ CRT⇣y

(·)ic

·$·,↵i

⌘

Per-Country Shape Parameters:

(↵i |�) ⇠ �

✏0 +

CX

c=1

`ic, ✏0 +CX

c=1

g

�⇠ic �i

�1�!

Per-Country Rate Parameters:

(�i |�) ⇠ �

✏0 + C↵i, ✏0 +

CX

c=1

✓ic

!

Diagonal Elements of the Core Tensor:

!

(r)c �k ⌘ ⌘

�

c ⌘$c ⌫k⇢r

y

(r)c �k ⌘

VX

i=1

X

j 6=i

AX

a=1

TX

t=1

y

(tr)

icak�!cj

⇠

(r)c �k ⌘

VX

i=1

✓ic

X

j 6=i

✓jc

AX

a=1

�ak

TX

t=1

tr b(t)

ia�!j

⇣�

(r)c �k |�

⌘⇠ �

⇣!

(r)c �k + y

(r)c �k , � + ⇠

(r)c �k⌘

6

Off-Diagonal Elements of the Core Tensor:

!

(r)

ck�!d

⌘ ⌘

$c ⌘

$d ⌫k⇢r c 6= d

y

(r)

ck�!d

⌘VX

i=1

X

j 6=i

AX

a=1

TX

t=1

y

(tr)

icak�!dj

c 6= d

⇠

(r)

ck�!d

⌘VX

i=1

✓ic

X

j 6=i

✓jd

AX

a=1

�ak

TX

t=1

tr b(t)

ia�!j

c 6= d

✓�

(r)

ck�!d

|�◆

⇠ �

✓!

(r)

ck�!d

++y

(r)

ck�!d

, � + ⇠

(r)

ck�!d

◆c 6= d

Core Rate Parameter:

!

(·)· ·$·

⌘CX

c=1

KX

k=1

RX

r=1

0

@!

(r)c �k +

X

d 6=c

!

(r)

ck�!d

1

A

�

(·)· ·$·

⌘CX

c=1

KX

k=1

RX

r=1

0

@�

(r)c �k +

X

d 6=c

�

(r)

ck�!d

1

A

(� |�) ⇠ �⇣✏0 + !

(·)· ·$·

, ✏0 + �

(·)· ·$·

⌘

Diagonal Auxiliary Latent Core Counts:

`

(r)c �k ⇠ CRT

⇣y

(r)c �k ,!

(r)c �k

⌘

Off-Diagonal Auxiliary Latent Core Counts:

`

(r)

ck�!d

⇠ CRT✓y

(r)

ck�!d

,!

(r)

ck�!d

◆c 6= d

Within-Community Weights:

`

(·)c � · ⌘

KX

k=1

RX

r=1

`

(r)c �k

⇠

�

c ⌘RX

r=1

⇢r

KX

k=1

⌫k

X

d 6=c

⌘

$d

✓g

✓⇠

(r)

ck�!d

�

�1

◆+ g

✓⇠

(r)

dk�!c

�

�1

◆◆

(⌘ �

c |�) ⇠ �⇣�0

C

+ `

(·)c � · , ⇣ + ⇠

�

c

⌘

7

Between-Community Weights:

`

(·)c

·$·⌘ `

(·)c � · +

X

d 6=c

KX

k=1

RX

r=1

✓`

(r)

ck�!d

+ `

(r)

dk�!c

◆

⇠

$c ⌘

RX

r=1

⇢r

KX

k=1

⌫k

2

4⌘

�

c g

⇣⇠

(r)c �k �

�1⌘+X

d 6=c

⌘

$d

✓g

✓⇠

(r)

ck�!d

�

�1

◆+ g

✓⇠

(r)

dk�!c

�

�1

◆◆3

5

(⌘$c |�) ⇠ �⇣�0

C

+ `

(·)c

·$·, ⇣ + ⇠

$c

⌘

Topic Weights:

`

(·)

·k�!·

⌘CX

c=1

CX

d=1

RX

r=1

`

(r)

ck�!d

⇠k ⌘RX

r=1

⇢r

CX

c=1

⌘

$c

2

4⌘

�

c g

⇣⇠

(r)c �k �

�1⌘+X

d 6=c

⌘

$d

✓g

✓⇠

(r)

ck�!d

�

�1

◆+ g

✓⇠

(r)

dk�!c

�

�1

◆◆3

5

(⌫k |�) ⇠ �

✓�0

K

+ `

(·)

·k�!·

, ⇣ + ⇠k

◆

Regime Weights:

`

(r)

··�!·

⌘CX

c=1

CX

d=1

KX

k=1

`

(r)

ck�!d

⇠r ⌘KX

k=1

⌫k

CX

c=1

⌘

$c

2

4⌘

�

c g

⇣⇠

(r)c �k �

�1⌘+X

d 6=c

⌘

$d

✓g

✓⇠

(r)

ck�!d

�

�1

◆+ g

✓⇠

(r)

dk�!c

�

�1

◆◆3

5

(⇢r |�) ⇠ �⇣�0

R

+ `

(r)

··�!·, ⇣ + ⇠r

⌘

Weights Rate Parameter:

! ⌘CX

c=1

⌘

�

c +CX

c=1

⌘

$c +

KX

k=1

⌫k+RX

r=1

⇢r

(⇣ |�) ⇠ � (✏0 + 4�0, ✏0 + !)

8

4 Baseline Models

BPTF (Schein et al., 2015):

y

(t)

ia�!j

⇠ Po

QX

q=1

✓

!iq ✓ jq �aq tq �q

!

✓

!iq ⇠ � (✏0,�1)

✓

jq ⇠ � (✏0,�2)

�aq ⇠ � (✏0,�3)

tq ⇠ � (✏0,�4)

�q ⇠ �

✓�0

Q

, �

◆

�1, · · · ,�4, � ⇠ � (✏0, ✏0)

GPIRM (Schmidt & Mørup, 2013):

y

(t)

ia�!j

⇠ Po✓�

(zt)

ziza�!zj

◆

zi ⇠ Cat✓

⌘1Pc ⌘c

, . . . ,

⌘CPc ⌘c

◆

za ⇠ Cat✓

⌫1Pk ⌫k

, . . . ,

⌫KPk ⌫k

◆

zt ⇠ Cat✓

⇢1Pr ⇢r

, . . . ,

⇢RPr ⇢r

◆

⌘c ⇠ �⇣�0

C

, ⇣

⌘

⌫k ⇠ �⇣�0

K

, ⇣

⌘

⇢r ⇠ �⇣�0

R

, ⇣

⌘

�

(r)

ck�!d

, ⇣ ⇠ � (✏0, ✏0)

DCGPIRM:

y

(t)

ia�!j

⇠ Po✓✓i ✓j �a t �

(zt)

ziza�!zj

◆

✓i,�a, t ⇠ �(✏0, ✏0)

The rest of the generative process is the same as that of the GPIRM.

9

5 Supplementary Plots

Figure 1: Inferred community weights ⌘

$1 , . . . , ⌘

$C . We use the between-community weights to

interpret shrinkage because they are used for the on- and off-diagonal elements of the core tensor.

References

Kingman, J. F. C. Poisson Processes. Oxford University Press, 1972.

Schein, A., Paisley, J., Blei, D. M., and Wallach, H. Bayesian Poisson tensor factorization for in-ferrring multilateral relations from sparse dyadic event counts. In Proceedings of the Twenty-First

ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 1045–1054,2015.

Schmidt, M. N. and Mørup, M. Nonparametric Bayesian modeling of complex networks: Anintroduction. IEEE Signal Processing Magazine, 30(3):110–128, 2013.

Zhou, M. Infinite edge partition models for overlapping community detection and link prediction.In Proceedings of the Eighteenth International Conference on Artificial Intelligence and Statistics, pp.1135–1143, 2015.

Zhou, M. and Carin, L. Negative binomial process count and mixture modeling. IEEE Transactions

on Pattern Analysis and Machine Intelligence, 37(2):307–320, 2015.

10

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

2019

1817

1615

1413

1211

109

87

65

43

21

UkraineGeorgia

AzerbaijanArmenia




CubaMexico

ColombiaChile

ArgentinaBrazil

VenezuelaPeru




LithuaniaLatvia




TajikistanTaiwan




LebanonIsrael


Saudi ArabiaSyria

EgyptJordanJapan


BelarusRussiaChina


IndiaIraq


UKUSA

USA U

KIre

land

Serb

iaK

osov

oB

osni

aA

lban

iaC

roat

iaIra

qIn

dia

Sri L

anka

Paki

stan

Ban

glad

esh

Chi

naR

ussi

aB

elar

usSo

uth

Kor

eaN

orth

Kor

eaJa

pan

Jord

anEg

ypt

Syria

Saud

i Ara

bia

Alg

eria

Yem

enK

uwai

tFr

ance

Isra

elLe

bano

nPa

lest

ine

Cyp

rus

Gre

ece

Turk

eyM

aced

onia

Mya

nmar

Cam

bodi

aTh

aila

ndVi

etna

mM

alay

sia

Phili

ppin

esSi

ngap

ore

Taiw

anTa

jikis

tan

Afg

hani

stan

Kyr

gyzs

tan

Uzb

ekis

tan

Kaz

akhs

tan

Iran

Hun

gary

Slov

akia

Cze

ch R

ep.

Aus

tria

Pola

ndR

oman

iaLa

tvia

Lith

uani

aB

elgi

umB

ulga

riaN

ethe

rland

sG

erm

any

Hol

y Se

eIta

lySw

itzer

land

Indo

nesi

aA

ustr

alia

New

Zea

land

Port

ugal

Peru

Vene

zuel

aB

razi

lA

rgen

tina

Chi

leC

olom

bia

Mex

ico

Cub

aSp

ain

Can

ada

Zim

babw

eU

gand

aN

iger

iaSo

uth

Afr

ica

Ken

yaLi

bya

Som

alia

Ethi

opia

Suda

nA

rmen

iaA

zerb

aija

nG

eorg

iaU

krai

ne

Figure 2: Latent structure discovered by BPTD for topic k = 1 (mostly Verbal Cooperation ac-tion types) and the most active regime, including the community–community interaction network(bottom left), the rate at which each country acts as a sender (top left) and a receiver (bottom right)in each community, and the number of times each country i took an action associated with topic ktoward each country j during regime r (top right). We show only the most active 100 countries.

11

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

2019

1817

1615

1413

1211

109

87

65

43

21

UkraineGeorgia

AzerbaijanArmenia




CubaMexico

ColombiaChile

ArgentinaBrazil

VenezuelaPeru




LithuaniaLatvia




TajikistanTaiwan




LebanonIsrael


Saudi ArabiaSyria

EgyptJordanJapan


BelarusRussiaChina


IndiaIraq


UKUSA

USA U

KIre

land

Serb

iaK

osov

oB

osni

aA

lban

iaC

roat

iaIra

qIn

dia

Sri L

anka

Paki

stan

Ban

glad

esh

Chi

naR

ussi

aB

elar

usSo

uth

Kor

eaN

orth

Kor

eaJa

pan

Jord

anEg

ypt

Syria

Saud

i Ara

bia

Alg

eria

Yem

enK

uwai

tFr

ance

Isra

elLe

bano

nPa

lest

ine

Cyp

rus

Gre

ece

Turk

eyM

aced

onia

Mya

nmar

Cam

bodi

aTh

aila

ndVi

etna

mM

alay

sia

Phili

ppin

esSi

ngap

ore

Taiw

anTa

jikis

tan

Afg

hani

stan

Kyr

gyzs

tan

Uzb

ekis

tan

Kaz

akhs

tan

Iran

Hun

gary

Slov

akia

Cze

ch R

ep.

Aus

tria

Pola

ndR

oman

iaLa

tvia

Lith

uani

aB

elgi

umB

ulga

riaN

ethe

rland

sG

erm

any

Hol

y Se

eIta

lySw

itzer

land

Indo

nesi

aA

ustr

alia

New

Zea

land

Port

ugal

Peru

Vene

zuel

aB

razi

lA

rgen

tina

Chi

leC

olom

bia

Mex

ico

Cub

aSp

ain

Can

ada

Zim

babw

eU

gand

aN

iger

iaSo

uth

Afr

ica

Ken

yaLi

bya

Som

alia

Ethi

opia

Suda

nA

rmen

iaA

zerb

aija

nG

eorg

iaU

krai

ne

Figure 3: Latent structure discovered by BPTD for topic k=2 (Verbal Cooperation).

12

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

2019

1817

1615

1413

1211

109

87

65

43

21

UkraineGeorgia

AzerbaijanArmenia




CubaMexico

ColombiaChile

ArgentinaBrazil

VenezuelaPeru




LithuaniaLatvia




TajikistanTaiwan




LebanonIsrael


Saudi ArabiaSyria

EgyptJordanJapan


BelarusRussiaChina


IndiaIraq


UKUSA

USA U

KIre

land

Serb

iaK

osov

oB

osni

aA

lban

iaC

roat

iaIra

qIn

dia

Sri L

anka

Paki

stan

Ban

glad

esh

Chi

naR

ussi

aB

elar

usSo

uth

Kor

eaN

orth

Kor

eaJa

pan

Jord

anEg

ypt

Syria

Saud

i Ara

bia

Alg

eria

Yem

enK

uwai

tFr

ance

Isra

elLe

bano

nPa

lest

ine

Cyp

rus

Gre

ece

Turk

eyM

aced

onia

Mya

nmar

Cam

bodi

aTh

aila

ndVi

etna

mM

alay

sia

Phili

ppin

esSi

ngap

ore

Taiw

anTa

jikis

tan

Afg

hani

stan

Kyr

gyzs

tan

Uzb

ekis

tan

Kaz

akhs

tan

Iran

Hun

gary

Slov

akia

Cze

ch R

ep.

Aus

tria

Pola

ndR

oman

iaLa

tvia

Lith

uani

aB

elgi

umB

ulga

riaN

ethe

rland

sG

erm

any

Hol

y Se

eIta

lySw

itzer

land

Indo

nesi

aA

ustr

alia

New

Zea

land

Port

ugal

Peru

Vene

zuel

aB

razi

lA

rgen

tina

Chi

leC

olom

bia

Mex

ico

Cub

aSp

ain

Can

ada

Zim

babw

eU

gand

aN

iger

iaSo

uth

Afr

ica

Ken

yaLi

bya

Som

alia

Ethi

opia

Suda

nA

rmen

iaA

zerb

aija

nG

eorg

iaU

krai

ne

Figure 4: Latent structure discovered by BPTD for topic k=3 (Material Cooperation).

13

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

2019

1817

1615

1413

1211

109

87

65

43

21

UkraineGeorgia

AzerbaijanArmenia




CubaMexico

ColombiaChile

ArgentinaBrazil

VenezuelaPeru




LithuaniaLatvia




TajikistanTaiwan




LebanonIsrael


Saudi ArabiaSyria

EgyptJordanJapan


BelarusRussiaChina


IndiaIraq


UKUSA

USA U

KIre

land

Serb

iaK

osov

oB

osni

aA

lban

iaC

roat

iaIra

qIn

dia

Sri L

anka

Paki

stan

Ban

glad

esh

Chi

naR

ussi

aB

elar

usSo

uth

Kor

eaN

orth

Kor

eaJa

pan

Jord

anEg

ypt

Syria

Saud

i Ara

bia

Alg

eria

Yem

enK

uwai

tFr

ance

Isra

elLe

bano

nPa

lest

ine

Cyp

rus

Gre

ece

Turk

eyM

aced

onia

Mya

nmar

Cam

bodi

aTh

aila

ndVi

etna

mM

alay

sia

Phili

ppin

esSi

ngap

ore

Taiw

anTa

jikis

tan

Afg

hani

stan

Kyr

gyzs

tan

Uzb

ekis

tan

Kaz

akhs

tan

Iran

Hun

gary

Slov

akia

Cze

ch R

ep.

Aus

tria

Pola

ndR

oman

iaLa

tvia

Lith

uani

aB

elgi

umB

ulga

riaN

ethe

rland

sG

erm

any

Hol

y Se

eIta

lySw

itzer

land

Indo

nesi

aA

ustr

alia

New

Zea

land

Port

ugal

Peru

Vene

zuel

aB

razi

lA

rgen

tina

Chi

leC

olom

bia

Mex

ico

Cub

aSp

ain

Can

ada

Zim

babw

eU

gand

aN

iger

iaSo

uth

Afr

ica

Ken

yaLi

bya

Som

alia

Ethi

opia

Suda

nA

rmen

iaA

zerb

aija

nG

eorg

iaU

krai

ne

Figure 5: Latent structure discovered by BPTD for topic k=4 (Verbal Conflict).

14

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

2019

1817

1615

1413

1211

109

87

65

43

21

UkraineGeorgia

AzerbaijanArmenia




CubaMexico

ColombiaChile

ArgentinaBrazil

VenezuelaPeru




LithuaniaLatvia




TajikistanTaiwan




LebanonIsrael


Saudi ArabiaSyria

EgyptJordanJapan


BelarusRussiaChina


IndiaIraq


UKUSA

USA U

KIre

land

Serb

iaK

osov

oB

osni

aA

lban

iaC

roat

iaIra

qIn

dia

Sri L

anka

Paki

stan

Ban

glad

esh

Chi

naR

ussi

aB

elar

usSo

uth

Kor

eaN

orth

Kor

eaJa

pan

Jord

anEg

ypt

Syria

Saud

i Ara

bia

Alg

eria

Yem

enK

uwai

tFr

ance

Isra

elLe

bano

nPa

lest

ine

Cyp

rus

Gre

ece

Turk

eyM

aced

onia

Mya

nmar

Cam

bodi

aTh

aila

ndVi

etna

mM

alay

sia

Phili

ppin

esSi

ngap

ore

Taiw

anTa

jikis

tan

Afg

hani

stan

Kyr

gyzs

tan

Uzb

ekis

tan

Kaz

akhs

tan

Iran

Hun

gary

Slov

akia

Cze

ch R

ep.

Aus

tria

Pola

ndR

oman

iaLa

tvia

Lith

uani

aB

elgi

umB

ulga

riaN

ethe

rland

sG

erm

any

Hol

y Se

eIta

lySw

itzer

land

Indo

nesi

aA

ustr

alia

New

Zea

land

Port

ugal

Peru

Vene

zuel

aB

razi

lA

rgen

tina

Chi

leC

olom

bia

Mex

ico

Cub

aSp

ain

Can

ada

Zim

babw

eU

gand

aN

iger

iaSo

uth

Afr

ica

Ken

yaLi

bya

Som

alia

Ethi

opia

Suda

nA

rmen

iaA

zerb

aija

nG

eorg

iaU

krai

ne

Figure 6: Latent structure discovered by BPTD for topic k=5 (Material Conflict).

15

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

2019

1817

1615

1413

1211

109

87

65

43

21

UkraineGeorgia

AzerbaijanArmenia




CubaMexico

ColombiaChile

ArgentinaBrazil

VenezuelaPeru




LithuaniaLatvia




TajikistanTaiwan




LebanonIsrael


Saudi ArabiaSyria

EgyptJordanJapan


BelarusRussiaChina


IndiaIraq


UKUSA

USA U

KIre

land

Serb

iaK

osov

oB

osni

aA

lban

iaC

roat

iaIra

qIn

dia

Sri L

anka

Paki

stan

Ban

glad

esh

Chi

naR

ussi

aB

elar

usSo

uth

Kor

eaN

orth

Kor

eaJa

pan

Jord

anEg

ypt

Syria

Saud

i Ara

bia

Alg

eria

Yem

enK

uwai

tFr

ance

Isra

elLe

bano

nPa

lest

ine

Cyp

rus

Gre

ece

Turk

eyM

aced

onia

Mya

nmar

Cam

bodi

aTh

aila

ndVi

etna

mM

alay

sia

Phili

ppin

esSi

ngap

ore

Taiw

anTa

jikis

tan

Afg

hani

stan

Kyr

gyzs

tan

Uzb

ekis

tan

Kaz

akhs

tan

Iran

Hun

gary

Slov

akia

Cze

ch R

ep.

Aus

tria

Pola

ndR

oman

iaLa

tvia

Lith

uani

aB

elgi

umB

ulga

riaN

ethe

rland

sG

erm

any

Hol

y Se

eIta

lySw

itzer

land

Indo

nesi

aA

ustr

alia

New

Zea

land

Port

ugal

Peru

Vene

zuel

aB

razi

lA

rgen

tina

Chi

leC

olom

bia

Mex

ico

Cub

aSp

ain

Can

ada

Zim

babw

eU

gand

aN

iger

iaSo

uth

Afr

ica

Ken

yaLi

bya

Som

alia

Ethi

opia

Suda

nA

rmen

iaA

zerb

aija

nG

eorg

iaU

krai

ne

Figure 7: Latent structure discovered by BPTD for topic k=6 (Material Conflict).

16

Bayesian Poisson Tucker Decomposition for Learning the ...aschein/ScheinZhouBleiWallach2016_paper.pdf1 c=1 P 1 d=1 P 1 k=1 P 1 r=1 (r) c! kd 1 c, d, , r from a gamma process, provided

Documents