2000__Calibration of Displacement Sensors Up to 300um With Nanometre Accuracy and Direct Traceability to a Primary Standard of Length

8/13/2019 2000__Calibration of Displacement Sensors Up to 300um With Nanometre Accuracy and Direct Traceability to a Pri

1/9

I metrologiaCalibration o displacement sensors up to 300 / Lmwith nanometre accuracy and direct traceabilityto a primary standard o lengthH. Haitjema P. H. J Schellekensnd S. F. C. L. Wetzels

Abstract. A new class of sensor has recently appeared: nanometre sensors. These sensors are characterized bynanometre or sub-nanometre resolution and an uncertainty of a few nanometres over a range of at least severalmicrometres. Instruments such as capacitive or inductive sensors, laser interferometers, holographic scales, andscanning probe microscopes belong to the class of nanometre sensors. Linearity errors and drift in the mechanicaland electronic system limit the accuracy of all these sensors. n order to determine these errors in a traceableway, the instrumentation described in this paper was developed. The heart of the system consists of a Fabry-Perotcavity. One mirror of this cavity generates the required displacement. A so-called slave laser is stabilized to thecavity length. The frequency of this slave laser is compared with the frequency of a primary length standard.In this way the displacement is measured with a resolution of few picometres, a range of 300 I m and anuncertainty of about 1 mn. Experiments confirm the performance of this instrument and show typical deviationsof the probe systems investigated.

1 IntroductionOwing to the tighter tolerances used in industry,demands on positioning accuracy are becoming increasingly higher [1]. Particularly in optics and electronics,error budgets are sometimes specified in terms ofnanometres. This has led to the development ofdisplacement sensors with accuracy in the range of1 nm and a resolution of sub-nanometre level.The working principle of these sensors can be of thecapacitive [2] or inductive type, but laser interferometersystems [3] and holographic scales [4] also euter thenanometre region where resolution is concerned. Theaccuracy of these systems is not self-evident fromtheir working principle. Effects such as proportionalityerrors, non-linearity and hysteresis can produce errors ofseveral nanometres even in sensors with sub-nanometreresolution. Careful design of the sensor minimizes theseerrors, but the problem of traceability remains. n orderto measure according to the definition of the metre,the sensor needs to be traceable to the standard oflength. This is achieved either by using a measuringprinciple cOlisisting of traceable elements only or bycalibrating the sensor on a traceable instrument. In the

H. Haitjema. P. H. J Schellekens and S. F. C. L Wetzels: PrecisionEngineering Section Eindhoven University o Technology POBox 654 W-hoog 1.107 2600 MB Eindhoven the Netherlands.Metrowgia. 2000. 37. 25-33

literature, several concepts of the latter method aredescribed, such as laser interferometers with enhancedinterpolation accuracy [3 5]. measuring lasers [6 7]and systems based on an external Fabry-Perot cavity[8-10]. This paper describes the latter approach.The vacuum wavelength of an iodine-stabilized HeNe laser is considered as a primary length standard [11].The wavelength of this laser is locked on the hyperfinestructure of 12712 This makes it possible to stabilize theabsolute vacuum wavelength of the laser to a level betterthan cUI) 10 10 Although this laser works very wellas a standard of length, it is not very practical as faras calibrating displacement sensors is concerned. Thelaser produces light of a certain wavelength, whereasthe sensors measure displacements. For calibrationpurposes an element is needed that connects wavelengthto displacement.One way of connecting wavelength to displacementis by directly calibrating sensors against the mirrorof a laser using the well-known relation betweenfrequency and displacement. Such a laser is calleda measuring laser [6 7] and has been realizedin the Precision Engineering Section of EindhovenUniversity of Technology. As the thermal instabilityof the laser resonator caused significant drift errorsin the calibration, it was decided to use an additionalexternal Fabry-Perot cavity instead, while maintainingthe primary standard laser for direct traceability.

25


2/9

H. Haitjema et al.

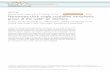
Preliminary results with such a system have beenreported elsewhere [8], using a provisional cavitywith a 10 fLm range and a non-continuous calibrationcapability. This paper gives measurements and a moreextensive description of the system with a 300 fLm rangeas it was finally realized. Also, calibration examplesare given which illustrate the capability of a continuousmeasurement over the full 300 fLm range.2. Optical layoutThe apparatus is based on a Fabry-Perot cavity to whicba laser is frequency-locked. Figure I schematicallydepicts the set-up. When oue of the mirrors of theFabry-Perot interferometer is displaced, the slave lasertracks the change in resonance frequency of the cavity.At the same time, a sensor to be calibrated is connectedto the mirror. The frequency counter measures thefrequency difference between the slave laser and theiodine-stabilized laser. A comparison of the sensor readout with the displacement derived from the frequencymeasurement gives the calibration data. This calibrationset-up is designed to give sub-nanometre resolution andaccuracy at nanometre level over a range of 300 fLm.The actual instrmnent on which the calibrationtakes place is a Fabry-Perot interferometer, consistingof two mirrors with a radius of 600 mm at a mutualdistance of 140 mm. The mirrors have a reflectivity, Rof R = 0.99. The resonance frequency, I where theFabry-Perot cavity transmits a maximum light intensityand reflects a minimum intensity, is described by

kc1= 2Ln I)where k is the mode number, c the speed of light, Lthe resonator length and n the refractive index of themedium inside the resonator.

iodine-stabilized laser

. I f one of the mirrors is displaced the resonatorlength will change by dL which gives a frequencychange dl according to I) of

dL dl-j (2)As the resonance frequency changes, a control

loop keeps the slave-laser frequency locked on thisresonance. Feedback for the control loop comes frommodulating the frequency of the slave laser overabout 20 MHz and phase-seusitive detection of the firstharmonic of the reflected signal from the Fabry-Perotcavity.The frequeucy change, dl, converts into displacement data, dL with (2) and is compared with theread-out of the sensor undergoing calibration. Thissensor is directly connected to the moving mirror ofthe Fabry-Perot cavity.For the calibration to be as accurate as possible,the slave laser must track the changing Fabry-Perotresonance as precisely as possible. The shape of theresonance curve plays an important role in trackingthe Fabry-Perot interferometer. The laser must alwaysbe locked on the same poiut of this curve. Mirrorreflectivity and losses inside the resouator determine itsshape, whereas the power of the laser light coupled intothe interferometer determines the absolute value of thereflected signal. The length of the resonator according to(2) ouly affects the position of the top of the resonancecurve. The uncertainty with which this locking can beachieved is discussed in Sectiou 3.3. Principle of measnrement over multiple modesFrom 2), it follows that the displacement that canbe tracked by the slave laser is limited by its tuningrange. For a given working range of the slave laser,dl, the tracked displacement, dL can be maximized by

avalanchem i d ~ p r i s ~ photodiodeFlf ICJ-. u . . "I-' mirror driver

1=001 I E:D:J:Ifrequeney counter

DIIltr In r;l }Y O : I-

slave laser F-P interferometercontrol loop photodiode=00

Figure 1. Schematic layout of the Fabry-Perot interferometer with slave laser.26

movingmirror/~ s o r

bendingrism

Metroiogia 2000, 37, 25 33


3/9

Calibration o displacf ment sensors up to 300 / Lm with nanometre ccur cy and direct traceability to a primary standard o length

I I ISituation 1

slave-laser modelocked on F-Presonance

n 21\ fF p

~ t ~ ~ = / _Situation 2 n+l n A n - l1\ ill 1\'- - .LLl.. > ~ ft P

IISituation 3 ,n 2 n + l n l n - l1\ 1\ A 1\ ft P

Situation 4 n 2 n + l n n - l1\ A 1\ 1\ ft PFigure 2 rocedure of locking the slave laser on successive modeschoosing the cavity length to be as large as possible. Fora desired measuring range of 300 fLm this would resultiu a cavity length that is impracticably long (14 m) anda proportional loss in resolution. In order to measureover a long range with a limited working range of theslave laser, successive resonance modes of the FabryPerot interferometer are tracked. Figure 2 shows howthis is achieved.In situation I, the slave laser is positioned at thestart of its working range and locked on the FabryPerot mode n. In case the mirror is displaced, allmodes are shifted in frequency according to (2). Theslave laser (situation 2) tracks the shift o f mode n.This continues until the slave laser reaches the endof its working range (situation 3). At this point theslave laser is unlocked from mode n and tuned overthe free spectral range (FSR) to mode n 1. Thenthe slave laser is locked on this mode (situation 4).The frequency difference between each mode is c/2L.Substituting this value in (2) yields a displacement ofMetroiagia 2000, 37, 25-33

A/2. This means that a calibration over a longer rangewill consist of tracking successive modes, each overA/2. Because the wavelength A is known accuratelyenongh from the frequency and the air refractiveindex), the discontinuities caused by the locking andunlocking do not affect the accuracy of the calibration.

f successive modes are to be successfully tracked,the slave laser must be able to be tuned from oneFabry-Perot mode to the next. This means that the laserworking range has to be larger than the FSR of theFabry-Perot interferometer. The working range of theslave laser is limited by the gain curve of neon; inpractice the laser working range is about 1200 MHz.The FSR of the Fabry-Perot interferometer must beadapted to this. From (2) follows a minimum cavitylength of 125 mm for the Fabry-Perot interferometer.In order to have enough margin, 140 mm was chosen forthe resonator length, which gives an FSR of 1071 MHz.The complete procedure of tracking, locking andunlocking is computer controlled.

27


4/9

H Haitjema et al

' ~ ~ : . . . . sensor lOop

resonator loop

Figure 3. Thermal loops in the construction of theFabry-Perot interferometer.4. Configuration and constructionof the interferometerCalibrating with the metrological Fabry-Perot interferometer basically consists of a comparison of the lengthsof two constrnctionalloops: one includes the sensor, theother the resonator (Figure 3). n uncontrolled changein the length of either of these loops introduces ameasurement error. Therefore the mechanical stabilityof the loops is essential to the accuracy of thecalibration. To achieve the desired accuracy of I nm,the length of the loops may not change more thanI nm within the measurement time of 15 minutes.The design of the constrnction is therefore aimed atmaximum stability.Figure 4 is a schematic drawing of the layout. TheFabry-Perot interferometer is positioned vertically on aframe in which the slave laser is placed horizontally.

moving mirrorZerodurrod

vacuum tube

frameslave laser fixed mirror

Figure 4. Mechanical layout of the Fabry-Perot interferometer.28

A polarizing prism bends the laser beam through 90For correct mode-matching, a lens is placed betweenlaser and interferometer.Translating the slave laser in the direction alignsthe laser and interferometer axis in the y direction.Alignment in the x direction is achieved by tranSlatingthe bending prism in x The optical axis of theinterferometer can be rotated by rotating the completeinterfetometer around the x and y axes with threeadjustment screws. n order to align the resonatormirrors relative to each other, the moving mirror canbe rotated around the x and y axes with an elastic tiltmechanism. The fixed mirror could be made adjustableinstead of the moving mirror. Making the movingmirror adjustable is advantageous. however, because itsadjustment mechanism is included in the constrnctionalloops of the interferometer as well as the sensor. Drift,which results from the adjustment mechanism, willtherefore be cancelled and will not cause calibrationerrors.The Fabry-Perot interferometer consists of a topplatform on which the sensor stands. The moving mirrorprotrndes through a hole in the centre of this platform.The mirror is mounted in the tilt-adjustment mechanism,which is fixed on to a parallel guiding mechanism. Thisallows a stroke of 300 I m. The fixed mirror is mountedon a platform at the underside of the interferometer.Three Zerodur rods are clamped between this platformand the upper calibration platform. In order to minimizethe influence of the refractive index of air on the opticallength of the resonator, an evacuated tube is placedover the lower mirror.A box that isolates acoustic as well as thermalfluctuations can be placed over the interferometer.Figure 5 gives a more detailed cross-sectionof the Fabry-Perot interferometer. The interferometerhas a resonator length of 140 mm which gives an

isolat ing box

bE.ndiDg prism

Metrologia 2000, 37. 25-33


5/9

Calibration o displacement sensors up to 300 jJ m with nanometre accuracy and direct traceability to a primary standard o length

pinhole

leafspringsbase cylinder

level t ~ ~ 7 ~ P ~ ~ ~ ~ ~ ~piezo-electric ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ Ipiezoscrew

vacuum tube

Zerodurrodfixed mirror

leafspringbottom platform

pre-tensioningfr me

slave-laser inputvacuum connection

Figure 5. Cross-section of the metrological Fabry-Perot interferometer.FSR of 1071 MHz. n experiments with a laser andinterferometer that were both variable in length, thislength was found to be the shortest possible to give agood match between the FSR nd the working rangeof the slave laserThe calibration takes place on the top platform,which has a diameter of 140 mm and, like most partsof the construction, is made from aluminium. t is boltedto the central body of the interferometer. As there is nointernal heat source, temperature differences betweendifferent parts will be almost zero. Parts made fromthe same material can therefore be clamped togetherwithout introducing thermal stresses.A platform with the fixed mirror is connected tothe underside of the central body by three bent leafsprings. The leaf springs accept expansion differencesbetween the central body made from aluminium and thethree rods made from Zerodur that are mounted betweenthe upper and lower platforms. The low-expansion rodsminimize the sensitivity to temperature changes of theconstructional loop of the interferometer.The moving mirror translates in an elastic guidingmechanism. The leaf springs have a length of 90 mm. norder to enhance the ratio between axial and transversalMetrologia 2000, 37, 25-33

stiffness, the middle part of the leaf springs is madethicker. The stiffness of the two leaf springs together inthe z direction is 4400 N/m o protect the leaf springsagainst overloading, a stroke-limiter is incorporated inthe design.As the two leaf springs each fix 3 degrees offreedom, the moving mirror is theoretically fixed in6 degrees of freedom. Because the leaf springs havealmost the same orientation, i.e. their compliant z axespractically coincide, the mirror can in practice movein the z direction with no problem. The behaviour ofthe guiding mechanism can however be made morepredictable by limiting the fixed degrees of freedom toonly 5. This is accomplished by connecting the twoleaf springs in a cross-shape. This geometry has a lowtorsional stiffness.aru:t thus 1 degree of freedom betweentheleaf springs is disconnected.A two-stage actuator drives the guiding mechanism.The first stage18 used for coarse adjustment and consistsof a piezo screw connected to a lever. This piezo screwis a commercial product based on a 0.5 mm pitch screwThe screw is slowly rotated in one direction by a piezoactuated clamp stepped over a very small displacement.Next, the clamp is rotated quickly in the other direction.

29


6/9

H aitjema et al

Owing to the inertia of the screw, the clamp slides overthe screw during this phase. By repeating this cycle,translations can be achieved over a very long range.The range is only limited by the length of the screwin combination with a resolution that is restricted bystick-slip phenomena. In practice, the screw can bepositioned with a resolution of about 100 urn. A leverwith a reduction ratio of 3 to I reduces this to about30 urn. The lever is made in one piece together withthe rest of the gniding mechanism by wire electricaldischarge machining. The hinges are of the elastic typewhich, together with the one-piece layout, means thatthe mechanism can be free of hysteresis and stiff, whilestill relatively simple.The lever is connected to the moving mirror viaa piezo-electric actuator. The piezo is used for finepositioning of the mirror in a range of 15 11m.The mirror is mounted on a ilt mechanism on topof the guiding mechanism. The tilt mechanism consistsof two elastic hinges that define two orthogonal axes ofrotation. The range of tilt is about 3 mrad.5. The slave laserThe slave laser is an existing laser design, developed atthe Precision Engineering Section, which was adaptedto give a maximum working range. For this purpose,experiments were carried out with different mirrorcurvatures, reflectivities and cavity lengths. Lengthwas found to be the most important of these factors.Best performance was achieved with a cavity lengthof 105 mm. The laser tube contains the isotope 22Neinstead of the usual 2oNe. This causes a shift of800 MHz of the gain profile of this isotope.As there is no overlap between slave and referencelaser, a displacement can be derived from the beatsignal in an unambignous way.6. Control loop and resolution achievedThe sharpness of the resonance curve is important forthe locking accuracy. This quality or finesse of theinterferometer is defined as the ratio of the width of theresonance curve and the distance between successiveresonance modes. The latter is the free spectral range(FSR) mentioned in Section 3.In practice, the finesse that is chosen is acompromise between accuracy and stability. Highfinesse means a sharp curve with a precisely definedlocking point. Low finesse means that the control loopis more flexible and will not easily jump out of lockbecause of a disturbance.

The control loop as indicated in Figure I consistsof a lock-in amplifier with a sinus generator anda Proportional-Integrating (PI) controller of the dcsteering signal. The sinus generator superimposes asinusoidal signal to the dc steering signal of onemirror of the slave laser. When the slave laser is30

t u ~ exactly on a transmission peak of the Fabry-Perotinterferometer, the lock-in amplifier measures zero andno steering signal is given. When the slave laser istuned on a flange of a peak, the lock-in amplifier givesa positive signal which is integrated and tunes the slavelaser towards the maximum intensity. The transmittedintensity, detector noise, amplitude of the sinus signal,and sharpness of the peak determine how accurately theslave laser can be tuned on an intensity peak.

As a measure of the sharpness of the transmissionpeak in a Fabry-Perot cavity, the finesse is commonlyused. The finesse is defined as the ratio between thefull width at half maximum (FWHM) of the resonancecurve and the FSR. For an ideal Fabry-Perot cavitywith concave mirrors with reflectance R the finesse Fis given by [12]F ~ 3- 2 y ~ )

Using R 0.99, we find F 300. This predictsa FWHM sharpness of the peak of about I urn. Inpractice, a larger FWHM of about 5 urn was found.This is illustrated in Figure 6, which shows the lockin output as a function of the displacement, using anoptimum modulation depth of 3 urn which correspondsto 10 MHz. This difference in finesse may be dueto scattering and local-geometry deviations of thecavity mirrors. Here, laser mirrors are used for whicha wave-front deformation of All0 is specified. Inhigh-finesse Fabry Perot interferometers, however, awave-front deformation of AIIOO or less is required.When stabilizing the laser to the cavity, i.e. to thezero crossing in Figure 6, the standard deviation inthe frequency difference with the standard laser wasISO kHz for a bandwidth of 10 Hz. This correspondsto a standard deviation of 0.05 om in length. Thisis the resolution that can basically be achieved ina calibration. As regards the uncertainty, many otherfactors are important and are discussed below.

1.0 .

> 0.5-;~ 0.0

0.5

1.0 v0 10 20 30 40 50Displacement I nmFigure 6. Output of the lock-in amplifier as a function of thedisplacement near an interference maximum

Metroiogia 2000, 37 25-33


7/9

Calibration ofdisplacement sensors up to 300 tJ m with nanometre accuracy nd direct traceability to a primary standard of ength

7. Thermal drift of the systemThe drift of the system is of major concern, as smalltemperature changes near a nanometre sensor can easilycause unwanted movements of several nanometres. Fora typical temperature change of 0.02 Clh, an errorof 1 nm is estimated considering the thermal lengthdifferences. This was confinned experimentally by thecalibration of several nanometre sensors: an inductiveprobe, capacitive probes and a laser interferometer.Figure 7 gives as an example a drift measurement of aninductive probe during nine hours. The figure shows aninitial drift in the first hour; the set-up becomes stablewith a remaining drift of about 1.5 nmJh.

108

E 6c4..20

-2 0 2 4 6 8 10Time h

Figure 7 Typical measurement of the drift of an inductiveprobe during nine hours

8. Uncertainty analysisAs illustrated in Section 6, the Fabry-Perot cavity offerssub-nanometre resolution owing to its high frequencyto displacement ratio. Other aspects are relevant to theuncertainty and are listed below (standard uncertainty,1 s .o The frequency measurement itself is accurate toabout 5 kHz with a gate time of 1 s. This causes anuncertainty in the calibration of about 0.005 nm.o The locking stability of the slave laser on theFabry-Perot cavity is limited by the zero stabilityin the electronics. Section 6 shows that this ischaracterized by a standard deviation of 0.05 nm.This includes (phase) shiftS in lock-in amplifiers.o The alignment of the displacement axes of themoving mirror and the sensor causes a cosine errorThis can be a major source of uncertainty when noalignment tool (e.g. auto-reflection, minimizing aMetrologia 2000 37 25-33

signal) is available and the alignment must be madevisually. For a typical 1misalignment, the cosineerror is 0.015 of the measured displacement. Anexperiment with an optimal visual alignment witha laser interferometer gave a deviation of 1 nm for30 fLm displacement.o Because a 9 mm air gap in the cavity is not

evacuated, there is still some uncompensated effectof the refractive index of air. During measurementslasting 15 minutes, the pressure was found tobe constant within 10 Pa (0.1 mbar), and thetemperature within 0.02 DC. This gives deviationsof 0.5 nm at maximum so as a standard uncertainty0.5 nmly 3 = 0.3 nm. Effects of humidity and CO2are much smaller. By measuring air temperature,air pressure and humidity, it is possible to virtuallyeliminate this uncertainty.

o The 2.5 mm thick Brewster window in the resonatorchanges its optical-path length by 0.3 nm fora temperature change of 0.02 DC. This gives astandard uncertainty of 0.2 nm.

o The limited thermomechanical stability of theconstruction introduces an uncertainty of, at most,0.2 nm during a normal calibration time of15 minutes. A thertual gradient change in the topplatform of 10-4 C results in a bending of 0.8 nmwhich mainly affects the top cavity mirror and notthe sensor. This gives a standard uncertainty of0.5 nm.

o The residual mirror tilt arising from the parallelgniding mechanism was measured to be 2.5 fLrad.This causes a deviation of 0.4 nm over 300 fLm.o As the gain profile of the slave laser is scannedduring a calibration, changes in the slope of thisprofile may cause deviations. An analysis showeda maximum deviation of 0.002 nm.o The resonator length was determined frommeasurements of the free spectral range (FSR). Therelative standard deviation in this determination

was 4 x 10-


8/9

H Haitjema et al

Table 1. Uncertainty budget for the Fabry-Perot nanomelresensor calibration system.Source Standard uncertainty ino uncertainty displacement/run

Displacement Displacement0.3 I ffi 300 jJ mFrequencymeasurement 0.005 0.005Locking noise 0.05 0.05Alignment 0.05 10Air gap 0.3 0.3Brewster window 0.2 0.2Thennomechanicalstability 0.5 0.5Mirror tilt 0.0004 0.4Laser gain profile 0.002 0.002Resonator length 0.13 0.13Refractive index 0.00006 0.06Total quadratic sum 0.6 10.02Uncertainty k = 2) 1.2 20in the set-up. For larger displacements, the alignmentbecomes the major source of uncertainty. This leadsto a deviation that is linear in length. Apart fromthis, the resolution remains a constaut 0.05 nm and theuncertainty in the deviation from linearity remains ofthe order of I nm. In future use of a nanometre sensor,alignment will be a similar source of uncertainty.9. Calibration examplesThe capability of the system in various ranges isillustrated by the calibration of capacitive probes inthe ranges of 0.7 11m, 10 I1ffi and 100 11m. The probesare PI types D-015.00 (15 11m range) and D-100.00(100 11m range). The probes showed a calibration errorof a few nanometres (0.5 ), 30 nm (0.3 ) and 4 11m4 ), in the respective calibration ranges. Figures 8,9 and 10 show the deviations from linearity measuredin the calibration, illustrating the capabilities of theset-up. The calibration factor appeared to be rathersensitive to the parallel alignment of the sensors, asknown from theory [2]. Figure 8 shows most clearlythe remaining combined noise from the calibrationsystem and the sensor. The repeated measurementsat the same displacement give a standard deviationof 0.08 nm; only slightly more than the predictednoise of 0.05 nm of the Fabry-Perot system. Figure 9gives the linearity deviations of the same probe ina range of 12 11m at four repeated measurements.The figure clearly illustrates a typical repeatable nonlinearity of a capacitive probe. The staudard deviationin the calibration points is 0.2 nm, probably caused bysome drift effects. Figure 10 also illustrates a significantnon-linearity, which however is not very large whenexpressed as a percentage (0.1 %).Further experiments were carried out with anatomic force microscope equipped with strain gaugesfor linearization (TopoMetrix TMX 2000 Explorer).32

0.40.3

E" 0.2" 0.10.0"?> -0.1c

:5 -0.2-0.3.-0.4

0 100 200 300 400 500 600 700 800Fabry Perot mirror displacement nm

Figure 8. Linearity deviation o a capacitive probe in arange of 700 mn.

4E 2"" 0'" -2CDCD" -4:::;

-60 2 4 6 8 10

Fabry Perot mirror displacement J..lmFigure 9. Linearity deviation o a capacitive probe in arange of 12 11ffi.

150100

E" 50" 0-80" -100

CD" -150:::;-200-250

0 20 40 80 80 100Fabry Perot mirror displacement J.lm

Figure 10. Linearity deviation o a capacitive probe in arange of 120 IJ-ffi.

12

120

Metrologia 2000. 37 25-33


9/9

Calibration ofdisplacement sensors up to 300 IJ.m with nanometre accuracy and direct traceability to a primary standardof length

This calibration clearly revealed some non-linearity1 ), hysteresis (1.5 ) and drift (0.05 nrn/s) of theinstrument, which is difficult to derive from normalmeasurements, not even by measuring referencespecimens.

Preliminary experiments were performed onthe non-linearity of laser interferometer systems.Depending on the a1igmnent and the set -up (planemirror or comer cube), linearity deviations between3 mn and 10 mn were found with a period of 157 mnor 315 nm. It is clear from the uncertainty budget andthe calibration results of the capacitive probes that thesedeviations must be attributed to the laser interferometersystem and its optics, and not to effects inside the cavityor to the slave laser (gain profile, frequency pulling).10. ConclusionsA calibration instrument for nanometre sensors has beenrealized with direct traceability to a primary lengthstandard. The range of 300 m, the resolution of0.05 nm and the final uncertainty of 1.2 mn for smalldisplacements, have been confirmed by calibrationexamples. This performance was achieved by anexternal Fabry-Perot cavity designed for maximumthermomechanical stability.Acknowledgements. The Dutch Technology Foundation (STW) and the NMi-Van Swinden Laboratorium(NMi-VSL) supported this research. Physik Instrumente, Waldbronn, Germany, are acknowledged formaking their sensors available for tests.

1. Schellekens P., Rosielle N., Venneulen J., VenneulenM., . Wetzels S. Pril W., Ann. College Internationalpour I Etude Scientifique des Techniques de ProductionMecanique CIRP), 1998, 47(2). 557-586.2. Heerens W. C J Phys. E: Sci. Instrum., 1986. 19897-906.

3. Downs M. J., Rowley W. R. C., Precis. Eng., 1993, 15281-286.4. Matsumo H., Minoshima K Opt. Commun.. 1996, 132,417-420.5. Basile G., Proc. 9th International Precision EngineeringSeminar, PTB, 1997, 248-259.6. Brand U., Hermann K., Meas. Sci. Technol 1996, 7911-917.7. Wetzels S. F. C. L., Schellekens P. H. J., Proc. IMEKO

TC 14, Lyngby, Denmark, 1996, 91-100.8. Wetzels S. F. C. L., Schellekens P. H. J., Ann. C1RP,1997, 46(1), 481-484.9. Howard L P., Scire F., Stone 1., Proc. Am. Soc. PrecisionEng. ASPE), 1996, 14, 385-390.

10. Haitjerna H., Rosielle N., Kolte G., Steijaert H., Meas.Sci. Techno ., 1998, 9 1098-1104.II Quinn T. J., Metrologia, 1993/94, 30. 523-541.12. Hecht E., Optics, 2nd ed., Reading, Mass., AddisonWesley, 1987, 676 p.13. Birch K. P., Downs M. J., Metrologia, 1994,31,315-316.

Received on 25 arch 1999 and in revised form on31 ay 1999.

2000__Calibration of Displacement Sensors Up to 300um With Nanometre Accuracy and Direct Traceability to a Primary Standard of Length

Documents