15

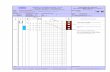
Nomenclature for a Typical xy Plot (Review)

Example Problem T5.2-7, Page 238 Write a program that plots the function for with a tick spacing of 0.25 on the x-axis and 2 on the y-axis.

1 1x− ≤ ≤

38y x=

Solution Plot the function for with a tick spacing of 0.25 on the x-axis and 2 on the y-axis. x=-1:0.01:1; y=8*x.^3; plot(x,y),set(gca,'xtick',-1:0.25:1,'ytick',-8:2:8) xlabel('x'),ylabel('y') gca: “Get Current Axes”

1 1x− ≤ ≤38y x=

Labeling Curves and Data The legend command automatically obtains from the plot the line type used for each data set and displays a sample of this line type in the legend box next to the string you selected. The following script file plots two functions with the corresponding legends (see next slide). x = 0:0.01:2; y = sinh(x); z = tanh(x); plot(x,y,x,z,’--’),xlabel(’x’), ... ylabel(’Hyperbolic Sine and Tangent’), ... legend(’sinh(x)’,’tanh(x)’)

Application of the legend Command

Application of the hold Command x = -1:0.01:1; y1 = 3+exp(-x).*sin(6*x); y2 = 4+exp(-x).*cos(6*x); plot((0.1+0.9i).^(0:0.01:10)),hold plot(y1,y2),gtext('y2 versus y1'),gtext('Imag(z) versus Real(z)')

Why Use Log Scales? Rectilinear scales cannot properly display variations over wide ranges. Next plot shows the missing information for the x-range of 0.1 to 10.

Rectangular Plot

A log-log plot can display wide variations in data values.

This plot shows the

same information as in the last plot for the small x-range of 0.1 to 10.

Why Use Log Scales? (cont.)

Logarithmic Plot

Logarithmic Plots 1. You cannot plot negative

numbers on a log scale, because the logarithm of a negative number is not defined.

2. You cannot plot the number 0 on a log scale, because log10 0 = ln 0 = −∞. You must choose an appropriate small number (e.g. 0.01) as the lower limit on the plot.

3. The tick-mark labels on a log scale are the actual values being plotted; they are not the logarithms of the numbers. For example, the range of x values in this plot is from 10−1 = 0.1 to 102 = 100.

Logarithmic Plots (cont.)

0.1 100

Logarithmic Plots (cont.)

4. Gridlines and tick marks within a decade are unevenly spaced.

If 8 gridlines or tick marks occur within the decade, they correspond to values equal to 2, 3, 4, . . . , 8, 9 times the value represented by the first gridline or tick mark of the decade. 2 x101 3 x101 4 x101

5. Equal distances on a log scale correspond to multiplication by the same constant (as opposed to addition of the same constant on a rectilinear scale).

Logarithmic Plots (cont.)

For example, all numbers that differ by a factor of 10 are separated by the same distance on a log scale. That is, the distance between 0.2 and 2 is the same as the distance between 3 and 30. This separation is referred to as a decade or cycle.

1. Use the loglog(x,y) command to have both scales logarithmic.

2. Use the semilogx(x,y) command to have the

x scale logarithmic and the y scale rectilinear. 3. Use the semilogy(x,y) command to have the

y scale logarithmic and the x scale rectilinear.

The appropriate command depends on which axis must have a log scale.

Types of Logarithmic Plots

Exponential and Power Functions Plotted on Log Scales x1 = 0:0.01:3; y1 = 25*exp(0.5*x1); y2 = 40*(1.7.^x1); x2 = logspace(-1,1,500); y3 = 15*x2.^(0.37); subplot(1,2,1),semilogy(x1,y1,x1,y2, '--'),... legend ('y = 25e^{0.5x}', 'y = 40(1.7) ^x'), .... xlabel('x'),ylabel('y'),grid on subplot(1,2,2),loglog(x2,y3),legend('y = 15x^{0.37}'), ... xlabel('x'),ylabel('y'), grid on

0 0.5 1 1.5 2 2.5 320

30

40

50

60

70

80

90

100

110

120

x1

y1

0.525 xy e=

0 0.37.5 40(1.7 2 1Ex ) 5 , 5aa nm ple d xx y xyy e= = =

The interactive plotting environment in MATLAB is a set of tools for:

• Creating different types of graphs, • Selecting variables to plot directly from the Workspace Browser, • Creating and editing subplots, • Adding annotations such as lines, arrows, text, rectangles, and

ellipses, and • Editing properties of graphics objects, such as their color, line weight,

and font.

Interactive Plotting in MATLAB

For details, see textbook pages 241-246.

The Figure and Plot Editor Toolbars

The Plot View interface includes the following three panels associated with a given figure.

· The Figure Palette: Use this to create and arrange

subplots, to view and plot workspace variables, and to add annotations.

· The Plot Browser: Use this to select and control the visibility of the axes or graphics objects plotted in the figure, and to add data for plotting.

· The Property Editor: Use this to set basic properties of the selected object and to obtain access to all properties through the Property Inspector.

The Figure Editor Toolbars (Cont.)

Exercise Create the following plot: >> t=1:0.1:100; >>y=sin(t); >>plot(t,y) Use the Plot View tools to: a) Add labels to the axes b) Change the color and thickness of the plot c) Generate and save the m-file for the modified plot

Exercise (Cont.)

1. Click on the axes to activate the window for

labeling

2. Click on the tabs to

add/change the axes labels

3. Click on the graph to activate the

window for color/thickness

4. Click on the available options

to change color/thickness

5. File > Generate Code…. The result is a function file (createfigure.m) that can be executed in the Command Window as: >> t=0:.1:10; >> y=sin(t); >>createfigure(t,y)

The following shows how to generate the surface plot of the function z = xe−[(x−y2)2+y2] , for −2 ≤ x ≤ 2 and −2 ≤ y ≤ 2, with a spacing of 0.1. [X,Y]= meshgrid(-2:0.1:2); Z = X.*exp(-((X-Y.^2).^2+Y.^2)); mesh(X,Y,Z),xlabel(’x’) ,... ylabel(’y’) zlabel(’z’)

Surface Plots (3D) – Example

Test Your Understanding P. 232: T5.2-2 through T5.2-5 P. 238: T5.2-6 P. 250: T5.4-1